Clark's triangle is a number triangle created by setting the vertex equal to 0, filling one diagonal with 1s, the other diagonal with multiples of an integer , and filling in the remaining entries by summing the elements on either side from one row above. The illustration above shows Clark's triangle for 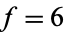 (OEIS A090850).

Call the first column 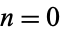 and the last column  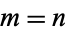so that

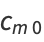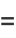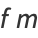			(1)
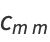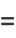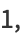			(2)

then use the recurrence relation

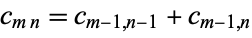(3)

to compute the rest of the entries. The result is given analytically by

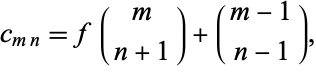(4)

where 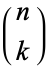 is a binomial coefficient (M. Alekseyev, pers. comm., Aug. 10, 2005).

The interesting part is that if 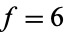 is chosen as the integer, then  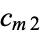and 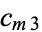 simplify to

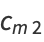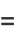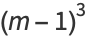			(5)
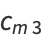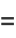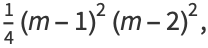			(6)

which are consecutive cubes 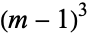 and nonconsecutive squares .

The sum of the 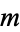th row for  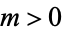is given by

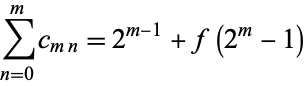(7)

(M. Alekseyev, pers. comm., Aug. 10, 2005).

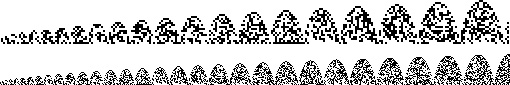
The plot above shows the binary representations for the first 255 (top figure) and 511 (bottom figure) terms of a flattened Clark's triangle with .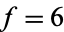

REFERENCES:

Clark, J. E. "Clark's Triangle." Math. Student 26, No. 2, p. 4, Nov. 1978.

Sloane, N. J. A. Sequence A090850 in "The On-Line Encyclopedia of Integer Sequences."