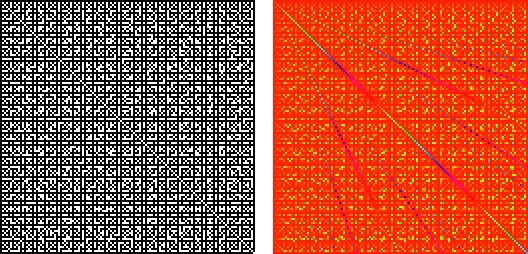
Two integers are relatively prime if they share no common positive factors (divisors) except 1. Using the notation  to denote the greatest common divisor, two integers  and  are relatively prime if . Relatively prime integers are sometimes also called strangers or coprime and are denoted . The plot above plots  and  along the two axes and colors a square black if  and white otherwise (left figure) and simply colored according to  (right figure).

Two numbers can be tested to see if they are relatively prime in the Wolfram Language using CoprimeQ[m, n].

Two distinct primes  and  are always relatively prime, , as are any positive integer powers of distinct primes  and , .

Relative primality is not transitive. For example,  and , but .

The probability that two integers  and  picked at random are relatively prime is

(1)

(OEIS A059956; Cesàro and Sylvester 1883; Lehmer 1900; Sylvester 1909; Nymann 1972; Wells 1986, p. 28; Borwein and Bailey 2003, p. 139; Havil 2003, pp. 40 and 65; Moree 2005), where  is the Riemann zeta function. This result is related to the fact that the greatest common divisor of  and , , can be interpreted as the number of lattice points in the plane which lie on the straight line connecting the vectors  and  (excluding  itself). In fact,  is the fractional number of lattice points visible from the origin (Castellanos 1988, pp. 155-156).

Given three integers  chosen at random, the probability that no common factor will divide them all is

(2)

(OEIS A088453; Wells 1986, p. 29), where  is Apéry's constant (Wells 1986, p. 29). In general, the probability that  random numbers lack a th power common divisor is  (Cohen 1959, Salamin 1972, Nymann 1975, Schoenfeld 1976, Porubský 1981, Chidambaraswamy and Sitaramachandra Rao 1987, Hafner et al. 1993).

Interestingly, the probability that two Gaussian integers  and  are relatively prime is

(3)

(OEIS A088454), where  is Catalan's constant (Pegg; Collins and Johnson 1989; Finch 2003, p. 601).

Similarly, the probability that two random Eisenstein integers are relatively prime is

(4)

(OEIS A088467), where

(5)

(Finch 2003, p. 601), which can be written analytically as

			(6)
			(7)

(OEIS A086724), where  is the trigamma function

Amazingly, the probabilities for random pairs of integers and Gaussian integers being relatively prime are the same as the asymptotic densities of squarefree integers of these types.

REFERENCES:

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.

Castellanos, D. "The Ubiquitous Pi." Math. Mag. 61, 67-98, 1988.

Chidambaraswamy, J. and Sitaramachandra Rao, R. "On the Probability That the Values of M Polynomials Have a Given G.C.D." J. Number Th. 26, 237-245, 1987.

Cohen, E. "Arithmetical Functions Associated with Arbitrary Sets of Integers." Acta Arith. 5, 407-415, 1959.

Collins, G. E. and Johnson, J. R. "The Probability of Relative Primality of Gaussian Integers." Proc. 1988 Internat. Sympos. Symbolic and Algebraic Computation (ISAAC), Rome (Ed. P. Gianni). New York: Springer-Verlag, pp. 252-258, 1989.

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 3-4, 1994.

Hafner, J. L.; Sarnak, P.; and McCurley, K. "Relatively Prime Values of Polynomials." In A Tribute to Emil Grosswald: Number Theory and Related Analysis (Ed. M. Knopp and M. Seingorn). Providence, RI: Amer. Math. Soc., 1993.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 38-39, 1998.

Lehmer, D. N. "An Asymptotic Evaluation of Certain Totient Sums." Amer. J. Math. 22, 293-355, 1900.

Moree, P. "Counting Carefree Couples." 30 Sep 2005. https://arxiv.org/abs/math.NT/0510003.

Nagell, T. "Relatively Prime Numbers. Euler's 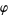-Function." §8 in Introduction to Number Theory. New York: Wiley, pp. 23-26, 1951.

Nymann, J. E. "On the Probability That 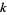 Positive Integers Are Relatively Prime." J. Number Th. 4, 469-473, 1972.

Nymann, J. E. "On the Probability That 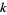 Positive Integers Are Relatively Prime. II." J. Number Th. 7, 406-412, 1975.

Pegg, E. Jr. "The Neglected Gaussian Integers." https://www.mathpuzzle.com/Gaussians.html.

Porubský, S. "On the Probability That K Generalized Integers Are Relatively H-Prime." Colloq. Math. 45, 91-99, 1981.

Salamin, E. Item 53 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 22, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item53.

Schoenfeld, L. "Sharper Bounds for the Chebyshev Functions 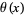 and 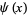, II." Math. Comput. 30, 337-360, 1976.

Sloane, N. J. A. Sequences A059956, A086724, A088453, A088454, and A088467 in "The On-Line Encyclopedia of Integer Sequences."

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 28-29, 1986.