The 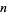-ball, denoted 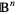, is the interior of a sphere 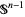, and sometimes also called the 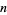-disk. (Although physicists often use the term "sphere" to mean the solid ball, mathematicians definitely do not!)

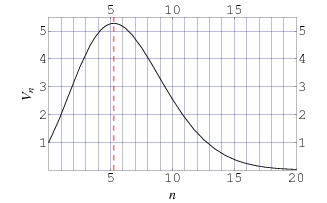
The ball of radius 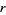 centered at point {x,y,z}" src="https://mathworld.wolfram.com/images/equations/Ball/Inline6.gif" style="height:15px; width:46px" /> is implemented in the Wolfram Language as Ball[{" src="https://mathworld.wolfram.com/images/equations/Ball/Inline7.gif" style="height:15px; width:5px" />x, y, z}" src="https://mathworld.wolfram.com/images/equations/Ball/Inline8.gif" style="height:15px; width:5px" />, r].

The equation for the surface area of the 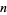-dimensional unit hypersphere  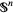gives the recurrence relation

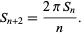(1)

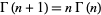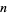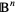Using  then gives the hypercontent of the -ball  of radiu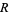s  as

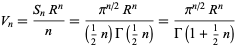(2)

(Sommerville 1958, p. 136; Apostol 1974, p. 430; Conway and Sloane 1993). Strangely enough, the content reaches a maximum and then decreases towards 0 as 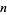 increases. The point of maximal content of a unit 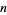-ball satisfies

			(3)
			(4)
			(5)

where 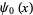 is the digamma function,  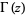is the gamma function,  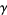is the Euler-Mascheroni constant, and  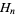is a harmonic number. This equation cannot be solved analytically for 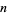, but the numerical solution to

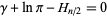(6)

is 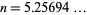 (OEIS A074455) (Wells 1986, p. 67). As a result, the five-dimensional unit ball  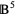has maximal content (Le Lionnais 1983; Wells 1986, p. 60).

The following table gives the content for the unit radius 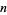-ball (OEIS A072345 and A072346), ratio of the volume of the 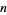-ball to that of a circumscribed hypercube (OEIS A087299), and surface area of the 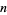-ball (OEIS A072478 and A072479).

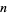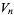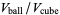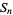0	1	1	0
1	2	1	2
2
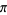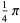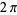3
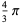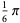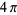4
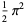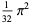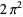5
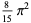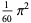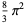6
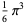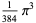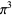7
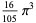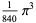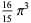8
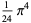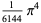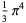9
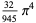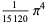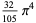10

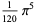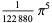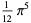Let 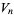 denote the volume of an 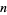-dimensional ball of radius 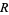. Then

			(7)
			(8)

so

(9)

where 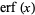 is the erf function (Freden 1993).

REFERENCES:

Apostol, T. M. Mathematical Analysis. Reading, MA: Addison-Wesley, 1974.

Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed. New York: Springer-Verlag, p. 9, 1993.

Freden, E. "Problem 10207: Summing a Series of Volumes." Amer. Math. Monthly 100, 882, 1993.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 58, 1983.

Sloane, N. J. A. Sequences A072345, A072346, A072478, A072479, A074455, and A087299 in "The On-Line Encyclopedia of Integer Sequences."

Sommerville, D. M. Y. An Introduction to the Geometry of n Dimensions. New York: Dover, p. 136, 1958.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.