Totient Function
The totient function  , also called Euler's totient function, is defined as the number of positive integers
, also called Euler's totient function, is defined as the number of positive integers  that are relatively prime to (i.e., do not contain any factor in common with)
that are relatively prime to (i.e., do not contain any factor in common with)  , where 1 is counted as being relatively prime to all numbers. Since a number less than or equal to and relatively prime to a given number is called a totative, the totient function
, where 1 is counted as being relatively prime to all numbers. Since a number less than or equal to and relatively prime to a given number is called a totative, the totient function 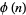 can be simply defined as the number of totatives of
can be simply defined as the number of totatives of 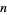 . For example, there are eight totatives of 24 (1, 5, 7, 11, 13, 17, 19, and 23), so
. For example, there are eight totatives of 24 (1, 5, 7, 11, 13, 17, 19, and 23), so 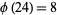 .
.
The totient function is implemented in the Wolfram Language as EulerPhi[n].
The number 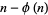 is called the cototient of
is called the cototient of 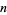 and gives the number of positive integers
and gives the number of positive integers 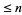 that have at least one prime factor in common with
that have at least one prime factor in common with 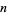 .
.
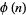 is always even for
is always even for 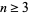 . By convention,
. By convention, 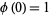 , although the Wolfram Language defines EulerPhi[0] equal to 0 for consistency with its FactorInteger[0] command. The first few values of
, although the Wolfram Language defines EulerPhi[0] equal to 0 for consistency with its FactorInteger[0] command. The first few values of 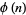 for
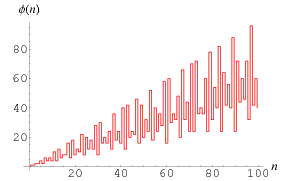
for 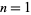 , 2, ... are 1, 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, ... (OEIS A000010). The totient function is given by the Möbius transform of 1, 2, 3, 4, ... (Sloane and Plouffe 1995, p. 22).
, 2, ... are 1, 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, ... (OEIS A000010). The totient function is given by the Möbius transform of 1, 2, 3, 4, ... (Sloane and Plouffe 1995, p. 22). 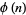 is plotted above for small
is plotted above for small 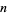 .
.
For a prime 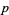 ,
,
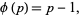 |
(1)
|
since all numbers less than 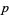 are relatively prime to
are relatively prime to 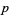 . If
. If 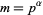 is a power of a prime, then the numbers that have a common factor with
is a power of a prime, then the numbers that have a common factor with 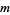 are the multiples of
are the multiples of 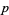 :
: 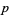 ,
, 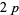 , ...,
, ..., 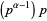 . There are
. There are 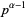 of these multiples, so the number of factors relatively prime to
of these multiples, so the number of factors relatively prime to 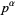 is
is
Now take a general 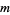 divisible by
divisible by 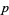 . Let
. Let 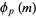 be the number of positive integers
be the number of positive integers 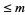 not divisible by
not divisible by 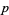 . As before,
. As before, 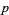 ,
, 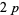 , ...,
, ..., 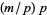 have common factors, so
have common factors, so
Now let 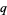 be some other prime dividing
be some other prime dividing 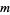 . The integers divisible by
. The integers divisible by 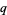 are
are 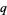 ,
, 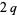 , ...,
, ..., 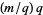 . But these duplicate
. But these duplicate 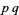 ,
, 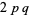 , ...,
, ..., 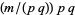 . So the number of terms that must be subtracted from
. So the number of terms that must be subtracted from 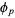 to obtain
to obtain 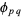 is
is
and
By induction, the general case is then
where the product runs over all primes 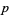 dividing
dividing 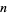 . An interesting identity relating
. An interesting identity relating 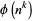 to
to 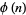 is given by
is given by
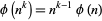 |
(14)
|
(A. Olofsson, pers. comm., Dec. 30, 2004).
Another identity relates the divisors 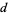 of
of 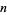 to
to 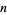 via
via
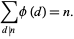 |
(15)
|
The totient function is connected to the Möbius function 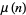 through the sum
through the sum
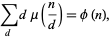 |
(16)
|
where the sum is over the divisors of 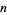 , which can be proven by induction on
, which can be proven by induction on 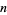 and the fact that
and the fact that 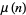 and
and 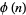 are multiplicative (Berlekamp 1968, pp. 91-93; van Lint and Nienhuys 1991, p. 123).
are multiplicative (Berlekamp 1968, pp. 91-93; van Lint and Nienhuys 1991, p. 123).
The totient function has the Dirichlet generating function
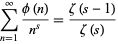 |
(17)
|
for 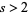 (Hardy and Wright 1979, p. 250).
(Hardy and Wright 1979, p. 250).
The totient function satisfies the inequality
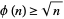 |
(18)
|
for all 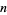 except
except 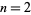 and
and 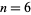 (Kendall and Osborn 1965; Mitrinović and Sándor 1995, p. 9). Therefore, the only values of
(Kendall and Osborn 1965; Mitrinović and Sándor 1995, p. 9). Therefore, the only values of 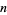 for which
for which 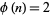 are
are 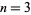 , 4, and 6. In addition, for composite
, 4, and 6. In addition, for composite 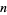 ,
,
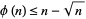 |
(19)
|
(Sierpiński and Schinzel 1988; Mitrinović and Sándor 1995, p. 9).
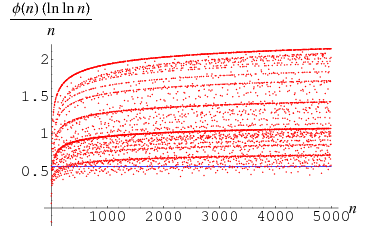
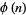 also satisfies
also satisfies
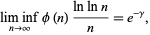 |
(20)
|
where 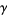 is the Euler-Mascheroni constant. The values of
is the Euler-Mascheroni constant. The values of 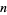 for which
for which 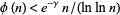 are given by 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 22, ... (OEIS A100966).
are given by 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 22, ... (OEIS A100966).
The divisor function satisfies the congruence
for all primes 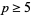 and no composite with the exception of 4, 6, and 22, where
and no composite with the exception of 4, 6, and 22, where 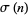 is the divisor function. This fact was proved by Subbarao (1974), despite the implication to the contrary, "is it true for infinitely many composite
is the divisor function. This fact was proved by Subbarao (1974), despite the implication to the contrary, "is it true for infinitely many composite 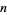 ?," stated in Guy (1994, p. 92), a query subsequently removed from Guy (2004, p. 142). No composite solution is currently known to
?," stated in Guy (1994, p. 92), a query subsequently removed from Guy (2004, p. 142). No composite solution is currently known to
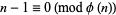 |
(23)
|
(Honsberger 1976, p. 35).
A corollary of the Zsigmondy theorem leads to the following congruence,
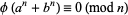 |
(24)
|
(Zsigmondy 1882, Moree 2004, Ruiz 2004ab).
The first few 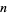 for which
for which
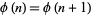 |
(25)
|
are given by 1, 3, 15, 104, 164, 194, 255, 495, 584, 975, ... (OEIS A001274), which have common values 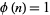 , 2, 8, 48, 80, 96, 128, 240, 288, 480, ... (OEIS A003275).
, 2, 8, 48, 80, 96, 128, 240, 288, 480, ... (OEIS A003275).
The only 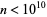 for which
for which
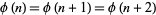 |
(26)
|
is 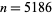 , giving
, giving
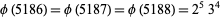 |
(27)
|
(Guy 2004, p. 139).
Values of 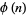 shared among
shared among 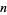 that are close together include
that are close together include
(Guy 2004, p. 139). McCranie found an arithmetic progression of six numbers with equal totient functions,
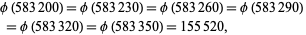 |
(32)
|
as well as other progressions of six numbers starting at 1166400, 1749600, ... (OEIS A050518).
If the Goldbach conjecture is true, then for every positive integer 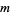 , there are primes
, there are primes 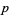 and
and 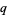 such that
such that
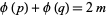 |
(33)
|
(Guy 2004, p. 160). Erdős asked if this holds for 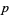 and
and 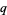 not necessarily prime, but this relaxed form remains unproven (Guy 2004, p. 160).
not necessarily prime, but this relaxed form remains unproven (Guy 2004, p. 160).
Guy (2004, p. 150) discussed solutions to
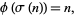 |
(34)
|
where 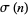 is the divisor function. F. Helenius has found 365 such solutions, the first of which are 2, 8, 12, 128, 240, 720, 6912, 32768, 142560, 712800, ... (OEIS A001229).
is the divisor function. F. Helenius has found 365 such solutions, the first of which are 2, 8, 12, 128, 240, 720, 6912, 32768, 142560, 712800, ... (OEIS A001229).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "The Euler Totient Function." §24.3.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 826, 1972.
Beiler, A. H. Ch. 12 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Berlekamp, E. R. Algorithmic Coding Theory. New York: McGraw-Hill, 1968.
Cohen, G. L. and Segal, S. L. "A Note Concerning Those 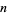 for which
for which 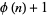 Divides
Divides 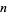 ." Fib. Quart. 27, 285-286, 1989.
." Fib. Quart. 27, 285-286, 1989.
Conway, J. H. and Guy, R. K. "Euler's Totient Numbers." The Book of Numbers. New York: Springer-Verlag, pp. 154-156, 1996.
Courant, R. and Robbins, H. "Euler's 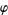 Function. Fermat's Theorem Again." §2.4.3 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 48-49, 1996.
Function. Fermat's Theorem Again." §2.4.3 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 48-49, 1996.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.
Guy, R. K. "Euler's Totient Function," "Does 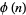 Properly Divide
Properly Divide 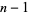 ," "Solutions of
," "Solutions of 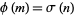 ," "Carmichael's Conjecture," "Gaps Between Totatives," "Iterations of
," "Carmichael's Conjecture," "Gaps Between Totatives," "Iterations of 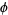 and
and 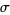 ," "Behavior of
," "Behavior of 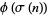 and
and 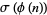 ." §B36-B42 in Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, pp. 138-151, 2004.
." §B36-B42 in Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, pp. 138-151, 2004.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 115-116, 2003.
Helenius, F. Untitled. http://pweb.netcom.com/~fredh/phisigma/pslist.html.
Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., p. 35, 1976.
Jones, G. A. and Jones, J. M. "Euler's Function." Ch. 5 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 83-96, 1998.
Kendall, D. G. and Osborn, R. "Two Simple Lower Bounds for Euler's Function." Texas J. Sci. 17, 1965.
Mitrinović, D. S. and Sándor, J. Handbook of Number Theory. Dordrecht, Netherlands: Kluwer, 1995.
Moree, P. "Phi Function Congruence." 13 Oct 2004. http://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0410&L=nmbrthry&T=0&F=&S=&P=1222.
Nagell, T. "Relatively Prime Numbers. Euler's 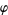 -Function." §8 in Introduction to Number Theory. New York: Wiley, pp. 23-26, 1951.
-Function." §8 in Introduction to Number Theory. New York: Wiley, pp. 23-26, 1951.
Niven, I. M.; Zuckerman, H. S.; and Montgomery, H. L. An Introduction to the Theory of Numbers, 5th ed. New York: Wiley, p. 51, 1991.
Perrot, J. 1811. Quoted in Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 126, 2005.
Ruiz, S. "A Congruence With the Euler Totient Function." 11 Oct 2004a. http://arxiv.org/abs/math.GM/0410241.
Ruiz, S. "Phi Function Congruence." 12 Oct 2004b. http://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0410&L=nmbrthry&T=0&F=&S=&P=834.
Séroul, R. "The Euler Phi Function." §2.7 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 14-15, 2000.
Shanks, D. "Euler's 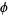 Function." §2.27 in Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 68-71, 1993.
Function." §2.27 in Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 68-71, 1993.
Sierpiński, W. and Schinzel, A. Elementary Theory of Numbers, 2nd Eng. ed. Amsterdam, Netherlands: North-Holland, 1988.
Sloane, N. J. A. Sequences A000010/M0299, A001229, A001274/M2999, A002088/M1008, A003275/M1874, A050518, and A100966 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, 1995.
Subbarao, M. V. "On Two Congruences for Primality." Pacific J. Math. 52, 261-268, 1974.
van Lint, J. H. and Nienhuys, J. W. Discrete Wiskunde.9062333680 Academic Service, 1991.
Zsigmondy, K. "Zur Theorie der Potenzreste." Monatshefte für Math. u. Phys. 3, 265-284, 1882.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


