A function 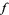 is said to be an entire modular form of weight  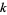if it satisfies

1. 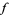 is analytic in the upper half-plane ,

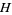2. 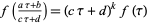 whenever  is a member of the modular group Gamma,

3. The Fourier series of 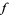 has the form

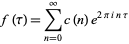(1)

Care must be taken when consulting the literature because some authors use the term "dimension 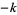" or "degree 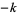" instead of "weight 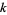," and others write  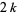instead of  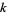(Apostol 1997, pp. 114-115). More general types of modular forms (which are not "entire") can also be defined which allow poles in  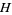or at 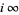. Since Klein's absolute invariant 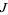, which is a modular function, has a pole at 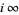, it is a nonentire modular form of weight 0.

The set of all entire forms of weight 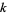 is denoted 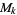, which is a linear space over the complex field. The dimension of  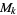is 1 for 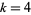, 6, 8, 10, and 14 (Apostol 1997, p. 119).

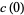 is the value of  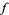at 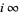, and if 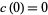, the function is called a cusp form. The smallest  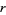such that  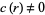is called the order of the zero of  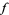at 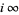. An estimate for  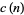states that

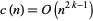(2)

if 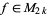 and is not a cusp form (Apostol 1997, p. 135).

If 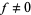 is an entire modular form of weigh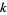t , let 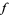 have 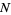 zeros in the closure of the fundamental region  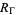(omitting the vertices). Then

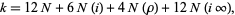(3)

where 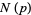 is the order of the zero at a point  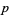(Apostol 1997, p. 115). In addition,

1. The only entire modular forms of weight 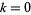 are the constant functions.

2. If 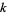 is odd, 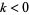, or 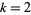, then the only entire modular form of weight  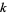is the zero function.

3. Every nonconstant entire modular form has weight 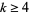, where  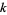is even.

4. The only entire cusp form of weight 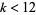 is the zero function.

(Apostol 1997, p. 116).

For 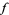 an entire modular form of even weight 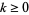, define  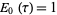for all . Then 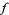 can be expressed in exactly one way as a sum

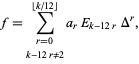(4)

where 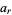 are complex numbers,  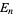is an Eisenstein series, and  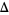is the modular discriminant of the Weierstrass elliptic function. cusp forms of even weight  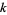are then those sums for which  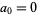(Apostol 1997, pp. 117-118). Even more amazingly, every entire modular form  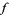of weight  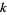is a polynomial in  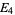and 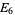 given by

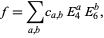(5)

where the 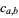 are complex numbers and the sum is extended over all integers  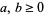such that  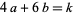(Apostol 1998, p. 118).

Modular forms satisfy rather spectacular and special properties resulting from their surprising array of internal symmetries. Hecke discovered an amazing connection between each modular form and a corresponding Dirichlet L-series. A remarkable connection between rational elliptic curves and modular forms is given by the Taniyama-Shimura conjecture, which states that any rational elliptic curve is a modular form in disguise. This result was the one proved by Andrew Wiles in his celebrated proof of Fermat's last theorem.

REFERENCES:

Apostol, T. M. "Modular Forms with Multiplicative Coefficients." Ch. 6 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 113-141, 1997.

Hecke, E. "Über Modulfunktionen und die Dirichlet Reihen mit Eulerscher Produktentwicklungen. I." Math. Ann. 114, 1-28, 1937.

Knopp, M. I. Modular Functions in Analytic Number Theory. New York: Chelsea, 1993.

Koblitz, N. Introduction to Elliptic Curves and Modular Forms. New York: Springer-Verlag, 1993.

Rankin, R. A. Modular Forms and Functions. Cambridge, England: Cambridge University Press, 1977.

Sarnack, P. Some Applications of Modular Forms. Cambridge, England: Cambridge University Press, 1993.