Min   Max       Re       Im

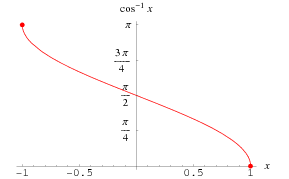
The inverse cosine is the multivalued function 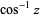 (Zwillinger 1995, p. 465), also denoted  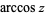(Abramowitz and Stegun 1972, p. 79; Harris and Stocker 1998, p. 307; Jeffrey 2000, p. 124), that is the inverse function of the cosine. The variants  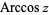(e.g., Beyer 1987, p. 141; Bronshtein and Semendyayev, 1997, p. 69) and  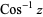are sometimes used to refer to explicit principal values of the inverse cosine, although this distinction is not always made (e.g,. Zwillinger 1995, p. 466). Worse yet, the notation  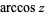is sometimes used for the principal value, with  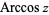being used for the multivalued function (Abramowitz and Stegun 1972, p. 80) Note that the notation  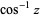(commonly used in North America and in pocket calculators worldwide),  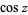is the cosine and the superscript  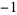denotes the inverse function, not the multiplicative inverse.

The principal value of the inverse cosine is implemented in the Wolfram Language as ArcCos[z] in the Wolfram Language. In the GNU C library, it is implemented as acos(double x).

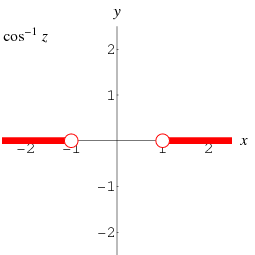
The inverse cosine is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at the line segments 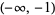 and 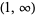. This follows from the definition of  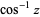as

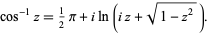(1)

Special values include

			(2)
			(3)
			(4)

The derivative of 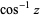 is given by

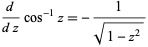(5)

and its indefinite integral is

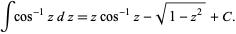(6)

The inverse cosine satisfies

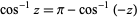(7)

for all complex 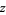, and

{1/2pi+cos^(-1)(sqrt(1-x^2)) for x<=0; 1/2pi-cos^(-1)(sqrt(1-x^2)) for x>=0. " src="http://mathworld.wolfram.com/images/equations/InverseCosine/NumberedEquation5.gif" style="height:76px; width:272px" />

(8)

The inverse cosine is given in terms of other inverse trigonometric functions by

			(9)
			(10)

for all complex ,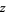

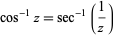(11)

for ,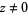

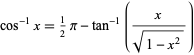(12)

for 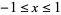, and

			(13)
			(14)
			(15)
			(16)

for 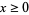, where in the last equation, equality at zero is understood to mean in the limit as .

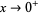The Maclaurin series for the inverse cosine with 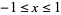 is

			(17)
			(18)

(OEIS A055786 and A002595).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 79-83, 1972.

Apostol, T. M. Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, pp. 254-255, 1967.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143 and 219, 1987.

Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. New York: Springer-Verlag, pp. 69-70, 1997.

GNU C Library. "Mathematics: Inverse Trigonometric Functions." http://www.gnu.org/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC389.

Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 307, 1998.

Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 124-128, 2000.

Sloane, N. J. A. Sequences A002595/M4233 and A055786 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.

Zwillinger, D. (Ed.). "Inverse Circular Functions." §6.3 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 465-467, 1995.