Min   Max       Re       Im

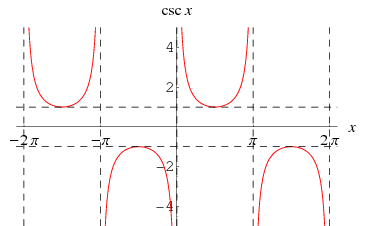
The cosecant 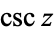 is the function defined by

			(1)
			(2)

where 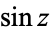 is the sine. The cosecant is implemented in the Wolfram Language as Csc[z].

The notation 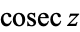 is sometimes also used (Gellert et al. 1989, p. 222; Gradshteyn and Ryzhik 2000, p. xxix). Note that the cosecant does not appear to be in consistent widespread use in Europe, although it does appear explicitly in various German and Russian handbooks (e.g., Gellert et al. 1989, p. 222; Gradshteyn and Ryzhik 2000, pp. xxix and p. 43). Interestingly, while  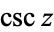is treated on par with the other trigonometric functions in some tabulations (Gellert et al. 1989, p. 222), it is not in others (Gradshteyn and Ryzhik 2000, who do not list it in their table of "basic functional relations" on p. 28, but do give identities involving it on p. 43).

Harris and Stocker (1998, p. 300) call secant and cosecant "rarely used functions," but then devote an entire section to them. Because these functions do seem to be in widespread use in the United States (e.g., Abramowitz and Stegun 1972, p. 72), reports of their demise seem to be a bit premature.

The derivative is

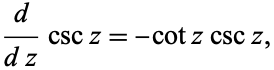(3)

and the indefinite integral is

(4)

where 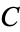 is a constant of integration. For  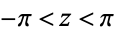on the real axis, this simplifies to

			(5)
			(6)

The Laurent series of the cosecant function is

			(7)
			(8)

(OEIS A036280 and A036281), where 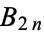 is a Bernoulli number.

The positive integer values of 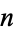 giving incrementally largest values of  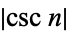are given by 1, 3, 22, 333, 355, 103993, ... (OEIS A046947), which are precisely the numerators of the convergents of  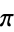and correspond to the values 1.1884, 7.08617, 112.978, 113.364, 33173.7, ....

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 71-79, 1972.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 215, 1987.

Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. New York: Van Nostrand Reinhold, 1989.

Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.

Harris, J. W. and Stocker, H. "Secant and Cosecant." §5.34 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, pp. 300-307, 1998.

Jeffrey, A. "Trigonometric Identities." §2.4 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 111-117, 2000.

Sloane, N. J. A. Sequences A036280, A036281, and A046947 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "The Secant 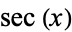 and Cosecant  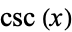Functions." Ch. 33 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 311-318, 1987.

Tropfke, J. Teil IB, §3. "Die Begriffe von Sekans und Kosekans eines Winkels." In Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter, fünfter Band, zweite aufl. Berlin and Leipzig, Germany: de Gruyter, pp. 28-30, 1923.

Zwillinger, D. (Ed.). "Trigonometric or Circular Functions." §6.1 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 452-460, 1995.