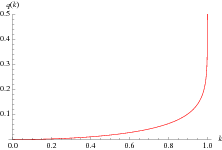
Given a Jacobi theta function, the nome is defined as

			(1)
			(2)
			(3)

(Borwein and Borwein 1987, pp. 41, 109 and 114), where  is the half-period ratio, 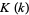 is the complete elliptic integral of the first kind, and  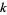is the elliptic modulus. The nome is implemented in the Wolfram Language as EllipticNomeQ[m].

Extreme care is needed when consulting the literature, as it is common in the theory of modular functions (and in particular the Dedekind eta function) to use the symbol 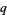 to denote 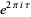, i.e., the square of the usual nome (e.g., Berndt 1993, p. 139). In this work, the modular version of  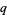is denoted

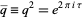(4)

(e.g., Borwein and Borwein 1987, p. 118).

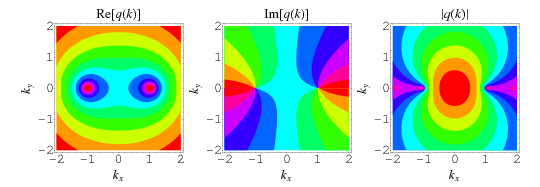
The nome in plotted above in the complex 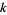-plane.

Various notations for Jacobi theta functions involving the nome include

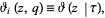(5)

where  is the half-period ratio (Whittaker and Watson 1990, p. 464) and

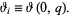(6)

Special values include

			(7)
			(8)
			(9)

The nome has Maclaurin series in parameter 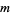 given by

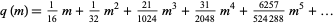(10)

(OEIS A002639 and A119349).

The nome has derivative

(11)

where 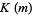 is a complete elliptic integral of the first kind and  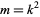is the elliptic modulus.

There exists a nonlinear third-order differential equation

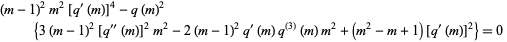(12)

for 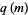 (Bertrand and Zudilin 2000; Trott 2006, pp. 29-31).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 591, 1972.

Berndt, B. C. Ramanujan's Theory of Theta-Functions, Theta Functions: from the Classical to the Modern. Providence, RI: Amer. Math. Soc., pp. 1-63, 1993.

Bertrand, D.; and Zudilin, W. "On the Transcendence Degree of the Differential Field Generated by Siegel Modular Forms." 23 Jun 2000. http://arxiv.org/abs/math.NT/0006176.

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.

Bramhall, J. N. "An Iterative Method for Inversion of Power Series." Comm. ACM 4, 317-318, 1961.

Ferguson, H. R. P.; Nielsen, D. E.; and Cook, G. "A Partition Formula for the Integer Coefficients of the Theta Function Nome." Math. Comput. 29, 851-855, 1975.

Fettis, H. E. "Note on the Computation of Jacobi's Nome and Its Inverse." Computing 4, 202-206, 1969.

Fletcher, A. §III in "Guide to Tables of Elliptic Functions." Math. Tables Other Aids Computation 3, 229-281, 1948.

"Guide to Tables." §III in Math. Tables Other Aids Computation 3, 234, 1948.

Hermite, C. Oeuvres, Vol. 4. Paris: Gauthier-Villars, p. 477, 1917.

Lowan, A. N.; Blanch, G.; and Horenstein, W. "On the Inversion of the 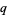-Series Associated with Jacobian Elliptic Functions." Bull. Amer. Math. Soc. 48, 737-738, 1942.

Sloane, N. J. A. Sequences A002639/M5108 and A119349 in "The On-Line Encyclopedia of Integer Sequences."

Tannery, J. and Molk, J. Eléments de la théorie des fonctions elliptiques, Vol. 4. Paris: Gauthier-Villars, p. 141, 1902.

Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.

Wang, Z. X. and Guo, D. R. Special Functions. Singapore: World Scientific, p. 512, 1989.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.