The Heaviside step function is a mathematical function denoted 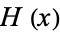, or sometimes  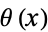or 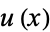 (Abramowitz and Stegun 1972, p. 1020), and also known as the "unit step function." The term "Heaviside step function" and its symbol can represent either a piecewise constant function or a generalized function.

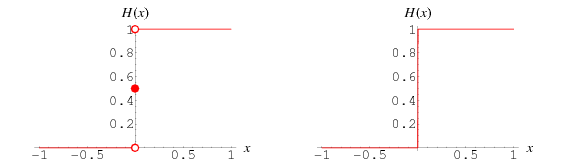
When defined as a piecewise constant function, the Heaviside step function is given by

{0 x<0; 1/2 x=0; 1 x>0 " src="http://mathworld.wolfram.com/images/equations/HeavisideStepFunction/NumberedEquation1.gif" style="height:70px; width:115px" />

(1)

(Abramowitz and Stegun 1972, p. 1020; Bracewell 2000, p. 61). The plot above shows this function (left figure), and how it would appear if displayed on an oscilloscope (right figure).

When defined as a generalized function, it can be defined as a function 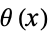 such that

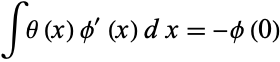(2)

for 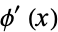 the derivative of a sufficiently smooth function  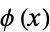that decays sufficiently quickly (Kanwal 1998).

The Wolfram Language represents the Heaviside generalized function as HeavisideTheta, while using UnitStep to represent the piecewise function Piecewise[{" src="http://mathworld.wolfram.com/images/equations/HeavisideStepFunction/Inline7.gif" style="height:15px; width:5px" />{" src="http://mathworld.wolfram.com/images/equations/HeavisideStepFunction/Inline8.gif" style="height:15px; width:5px" />1, x >= 0}" src="http://mathworld.wolfram.com/images/equations/HeavisideStepFunction/Inline9.gif" style="height:15px; width:5px" />}" src="http://mathworld.wolfram.com/images/equations/HeavisideStepFunction/Inline10.gif" style="height:15px; width:5px" />] (which, it should be noted, adopts the convention 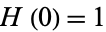 instead of the conventional definition ).

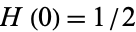The shorthand notation

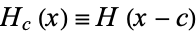(3)

is sometimes also used.

The Heaviside step function is related to the boxcar function by

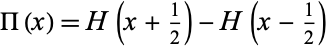(4)

and can be defined in terms of the sign function by

(5)

The derivative of the step function is given by

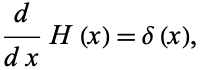(6)

where 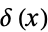 is the delta function (Bracewell 2000, p. 97).

The Heaviside step function is related to the ramp function 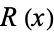 by

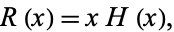(7)

and to the derivative of 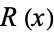 by

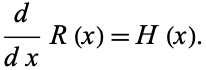(8)

The two are also connected through

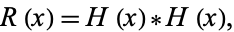(9)

where 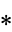 denotes convolution.

Bracewell (2000) gives many identities, some of which include the following. Letting 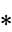 denote the convolution,

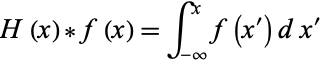(10)

			(11)
			(12)
			(13)
			(14)

In addition,

			(15)
		{H(x+b/a) a>0; H(-x-b/a) a<0." src="http://mathworld.wolfram.com/images/equations/HeavisideStepFunction/Inline35.gif" style="height:82px; width:124px" />	(16)

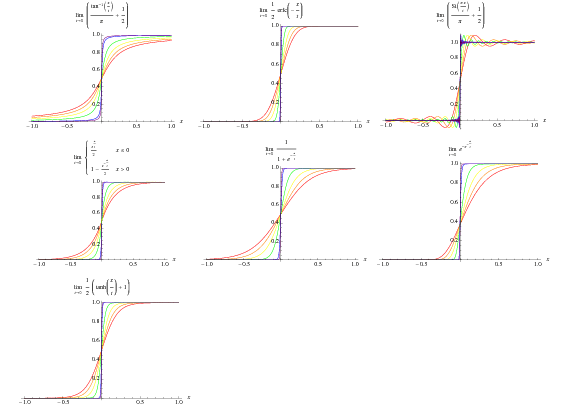
The Heaviside step function can be defined by the following limits,

			(17)
			(18)
			(19)
			(20)
			(21)
			(22)
		{1/2e^(x/t) for x<=0; 1-1/2e^(-x/t) for x>=0" src="http://mathworld.wolfram.com/images/equations/HeavisideStepFunction/Inline56.gif" style="height:56px; width:148px" />	(23)
			(24)
			(25)
			(26)
			(27)

where 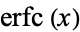 is the erfc function,  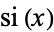is the sine integral,  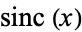is the sinc function, and  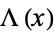is the one-argument triangle function. The first four of these are illustrated above for 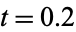, 0.1, and 0.01.

Of course, any monotonic function with constant unequal horizontal asymptotes is a Heaviside step function under appropriate scaling and possible reflection. The Fourier transform of the Heaviside step function is given by

			(28)
			(29)

where 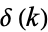 is the delta function.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.

Bracewell, R. "Heaviside's Unit Step Function, 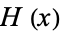." The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 61-65, 2000.

Kanwal, R. P. Generalized Functions: Theory and Technique, 2nd ed. Boston, MA: Birkhäuser, 1998.

Spanier, J. and Oldham, K. B. "The Unit-Step 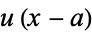 and Related Functions." Ch. 8 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 63-69, 1987.