
Weber Functions
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
"Anger and Weber Functions." §12.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
المصدر:
"Anger and Weber Functions." §12.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
 الجزء والصفحة:
...
الجزء والصفحة:
...
 14-9-2019
14-9-2019
 3320
3320
Weber Functions
Although Bessel functions of the second kind are sometimes called Weber functions, Abramowitz and Stegun (1972) define a separate Weber function as
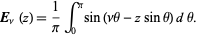 |
(1)
|
These function may also be written as
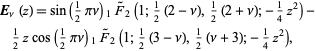 |
(2)
|
where 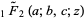 is a regularized hypergeometric function.
is a regularized hypergeometric function.
This function is implemented in the Wolfram Language as WeberE[nu, z] and is an analog of the Anger function.
Special values for real  include
include
where 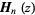 is a Struve function.
is a Struve function.
Letting 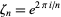 be a root of unity, another set of Weber functions is defined as
be a root of unity, another set of Weber functions is defined as
(Weber 1902, Atkin and Morain 1993), where 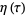 is the Dedekind eta function and
is the Dedekind eta function and  is the half-period ratio. These functions are related to the Ramanujan g- and G-functions and the elliptic lambda function.
is the half-period ratio. These functions are related to the Ramanujan g- and G-functions and the elliptic lambda function.
The Weber functions satisfy the identities
(Weber 1902, Atkin and Morain 1993).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Anger and Weber Functions." §12.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 498-499, 1972.
Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 68-69, 1987.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Anger Function 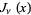 and Weber Function
and Weber Function 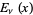 ." §1.5 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, p. 28, 1990.
." §1.5 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, p. 28, 1990.
Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, pp. 113-114, 1902.
Weng, A. "Class Polynomials of CM-Fields. http://www.exp-math.uni-essen.de/zahlentheorie/classpol/class.html.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


