

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Riemann Zeta Function zeta(2)
المؤلف:
Apostol, T. M.
المصدر:
"A Proof That Euler Missed: Evaluating zeta(2) the Easy Way." Math. Intel. 5
الجزء والصفحة:
...
13-9-2019
4157
Riemann Zeta Function zeta(2)
The value for
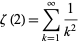 |
(1) |
can be found using a number of different techniques (Apostol 1983, Choe 1987, Giesy 1972, Holme 1970, Kimble 1987, Knopp and Schur 1918, Kortram 1996, Matsuoka 1961, Papadimitriou 1973, Simmons 1992, Stark 1969, 1970, Yaglom and Yaglom 1987).
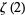 is therefore the definite sum version of the indefinite sum
is therefore the definite sum version of the indefinite sum
 |
 |
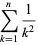 |
(2) |
 |
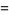 |
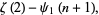 |
(3) |
where 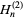 is a generalized harmonic number (whose numerator is known as a Wolstenholme number) and
is a generalized harmonic number (whose numerator is known as a Wolstenholme number) and 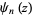 is a polygamma function.
is a polygamma function.
The problem of finding this value analytically is sometimes known as the Basel problem (Derbyshire 2004, pp. 63 and 370) or Basler problem (Castellanos 1988). It was first proposed by Pietro Mengoli in 1644 (Derbyshire 2004, p. 370). The solution
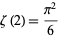 |
(4) |
was first found by Euler in 1735 (Derbyshire 2004, p. 64) or 1736 (Srivastava 2000).
Yaglom and Yaglom (1987), Holme (1970), and Papadimitriou (1973) all derive the result, 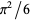 from de Moivre's identity or related identities.
from de Moivre's identity or related identities.
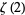 is given by the series
is given by the series
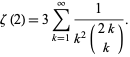 |
(5) |
(Knopp 1990, pp. 266-267), probably known to Euler and rediscovered by Apéry.
Bailey (2000) and Borwein and Bailey (2003, pp. 128-129) give a collection of BBP-type formulas that include a number for 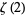 ,
,
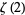 |
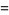 |
![(27)/4sum_(k=0)^(infty)1/(64^k)[(16)/((6k+1)^2)-(24)/((6k+2)^2)-8/((6k+3)^2)-6/((6k+4)^2)+1/((6k+5)^2)]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline15.gif) |
(6) |
 |
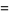 |
![4/9sum_(k=0)^(infty)1/(729^k)[(243)/((12k+1)^2)-(405)/((12k+2)^2)-(81)/((12k+4)^4)-(27)/((12k+5)^2)-(72)/((12k+6)^2)-9/((12k+7)^2)-9/((12k+8)^2)-5/((12k+10)^2)+1/((12k+11)^2)].](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline18.gif) |
(7) |
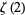 is given by the double series
is given by the double series
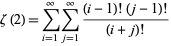 |
(8) |
(B. Cloitre, pers. comm., Dec. 9, 2004).
One derivation for 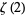 considers the Fourier series of
considers the Fourier series of 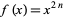
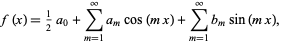 |
(9) |
which has coefficients given by
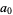 |
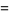 |
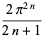 |
(10) |
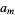 |
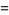 |
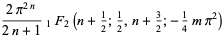 |
(11) |
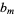 |
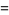 |
 |
(12) |
where 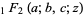 is a generalized hypergeometric function and (12) is true since the integrand is odd. Therefore, the Fourier series is given explicitly by
is a generalized hypergeometric function and (12) is true since the integrand is odd. Therefore, the Fourier series is given explicitly by
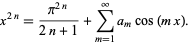 |
(13) |
If 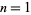 , then
, then
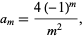 |
(14) |
so the Fourier series is
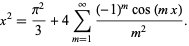 |
(15) |
Letting 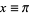 gives
gives 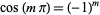 , so
, so
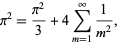 |
(16) |
and we have
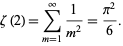 |
(17) |
Higher values of 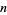 can be obtained by finding
can be obtained by finding 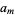 and proceeding as above.
and proceeding as above.
The value 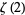 can also be found simply using the root linear coefficient theorem. Consider the equation
can also be found simply using the root linear coefficient theorem. Consider the equation 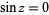 and expand sin in a Maclaurin series
and expand sin in a Maclaurin series
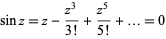 |
(18) |
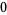 |
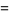 |
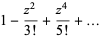 |
(19) |
 |
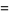 |
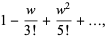 |
(20) |
where 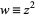 . But the zeros of
. But the zeros of 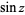 occur at
occur at 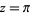 ,
, 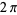 ,
, 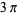 , ..., or
, ..., or 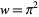 ,
, 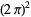 , .... Therefore, the sum of the roots equals the coefficient of the leading term
, .... Therefore, the sum of the roots equals the coefficient of the leading term
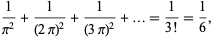 |
(21) |
which can be rearranged to yield
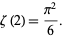 |
(22) |
Yet another derivation (Simmons 1992) evaluates 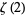 using Beukers's (1979) integral
using Beukers's (1979) integral
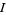 |
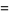 |
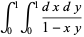 |
(23) |
 |
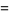 |
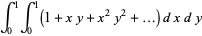 |
(24) |
 |
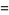 |
![int_0^1[(x+1/2x^2y+1/3x^3y^2+...)]_0^1dy](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline61.gif) |
(25) |
 |
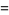 |
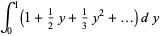 |
(26) |
 |
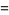 |
![[y+(y^2)/(2^2)+(y^3)/(3^2)+...]_0^1](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline67.gif) |
(27) |
 |
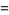 |
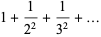 |
(28) |
 |
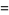 |
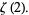 |
(29) |
To evaluate the integral, rotate the coordinate system by 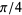 so
so
 |
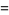 |
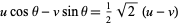 |
(30) |
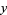 |
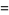 |
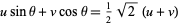 |
(31) |
and
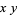 |
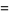 |
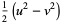 |
(32) |
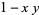 |
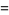 |
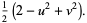 |
(33) |
Then
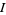 |
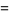 |
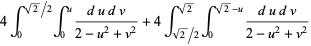 |
(34) |
 |
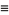 |
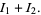 |
(35) |
Now compute the integrals 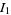 and
and 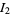 .
.
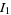 |
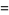 |
![4int_0^(sqrt(2)/2)[int_0^u(dv)/(2-u^2+v^2)]du](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline97.gif) |
(36) |
 |
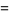 |
![4int_0^(sqrt(2)/2)[1/(sqrt(2-u^2))tan^(-1)(v/(sqrt(2-u^2)))]_0^udu](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline100.gif) |
(37) |
 |
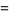 |
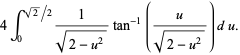 |
(38) |
Make the substitution
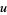 |
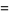 |
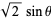 |
(39) |
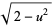 |
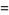 |
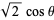 |
(40) |
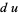 |
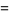 |
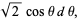 |
(41) |
so
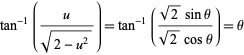 |
(42) |
and
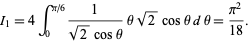 |
(43) |
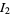 can also be computed analytically,
can also be computed analytically,
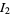 |
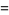 |
![4int_(sqrt(2)/2)^(sqrt(2))[int_0^(sqrt(2)-u)(dv)/(2-u^2+v^2)]du](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline116.gif) |
(44) |
 |
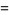 |
![4int_(sqrt(2)/2)^(sqrt(2))[1/(sqrt(2-u^2))tan^(-1)(v/(sqrt(2-u^2)))]_0^(sqrt(2)-u)du](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline119.gif) |
(45) |
 |
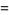 |
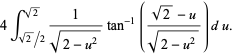 |
(46) |
But
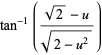 |
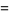 |
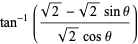 |
(47) |
 |
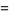 |
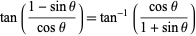 |
(48) |
 |
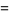 |
![tan^(-1)[(sin(1/2pi-theta))/(1+cos(1/2pi-theta))]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline131.gif) |
(49) |
 |
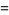 |
(50) |
|
 |
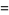 |
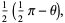 |
(51) |
so
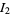 |
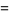 |
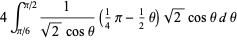 |
(52) |
 |
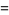 |
![4[1/4pitheta-1/4theta^2]_(pi/6)^(pi/2)](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline143.gif) |
(53) |
 |
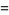 |
![4[((pi^2)/8-(pi^2)/(16))-((pi^2)/(24)-(pi^2)/(144))]=(pi^2)/9.](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeta2/Inline146.gif) |
(54) |
Combining 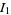 and
and 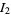 gives
gives
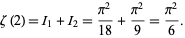 |
(55) |
REFERENCES:
Apostol, T. M. "A Proof That Euler Missed: Evaluating 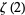 the Easy Way." Math. Intel. 5, 59-60, 1983.
the Easy Way." Math. Intel. 5, 59-60, 1983.
Bailey, D. H. "A Compendium of BBP-Type Formulas for Mathematical Constants." 28 Nov 2000. http://crd.lbl.gov/~dhbailey/dhbpapers/bbp-formulas.pdf.
Beukers, F. "A Note on the Irrationality of 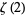 and
and 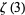 ." Bull. London Math. Soc. 11, 268-272, 1979.
." Bull. London Math. Soc. 11, 268-272, 1979.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 89-90, 2003.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.
Choe, B. R. "An Elementary Proof of 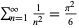 ." Amer. Math. Monthly 94, 662-663, 1987.
." Amer. Math. Monthly 94, 662-663, 1987.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Giesy, D. P. "Still Another Proof That 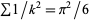 ." Math. Mag. 45, 148-149, 1972.
." Math. Mag. 45, 148-149, 1972.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 37-40, 2003.
Holme, F. "Ein enkel beregning av 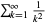 ." Nordisk Mat. Tidskr. 18, 91-92 and 120, 1970.
." Nordisk Mat. Tidskr. 18, 91-92 and 120, 1970.
Kimble, G. "Euler's Other Proof." Math. Mag. 60, 282, 1987.
Knopp, K. Theory and Application of Infinite Series. New York: Dover, 1990.
Knopp, K. and Schur, I. "Über die Herleitug der Gleichung 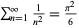 ." Archiv der Mathematik u. Physik 27, 174-176, 1918.
." Archiv der Mathematik u. Physik 27, 174-176, 1918.
Kortram, R. A. "Simple Proofs for 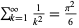 and
and 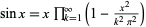 ." Math. Mag. 69, 122-125, 1996.
." Math. Mag. 69, 122-125, 1996.
Matsuoka, Y. "An Elementary Proof of the Formula 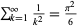 ." Amer. Math. Monthly 68, 486-487, 1961.
." Amer. Math. Monthly 68, 486-487, 1961.
Papadimitriou, I. "A Simple Proof of the Formula 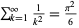 ." Amer. Math. Monthly 80, 424-425, 1973.
." Amer. Math. Monthly 80, 424-425, 1973.
Simmons, G. F. "Euler's Formula 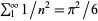 by Double Integration." Ch. B. 24 in Calculus Gems: Brief Lives and Memorable Mathematics. New York: McGraw-Hill, 1992.
by Double Integration." Ch. B. 24 in Calculus Gems: Brief Lives and Memorable Mathematics. New York: McGraw-Hill, 1992.
Spiess, O. "Die Summe der reziproken Quadratzahlen." In Festschrift zum 60 Geburtstag von Dr. Andreas Speiser (Ed. L. V. Ahlfors et al. ). Zürich: Füssli, pp. 66-86, 1945.
Srivastava, H. M. "Some Simple Algorithms for the Evaluations and Representations of the Riemann Zeta Function at Positive Integer Arguments." J. Math. Anal. Appl. 246, 331-351, 2000.
Stark, E. L. "Another Proof of the Formula 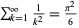 ." Amer. Math. Monthly 76, 552-553, 1969.
." Amer. Math. Monthly 76, 552-553, 1969.
Stark, E. L. "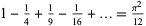 ." Praxis Math. 12, 1-3, 1970.
." Praxis Math. 12, 1-3, 1970.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 40, 1986.
Yaglom, A. M. and Yaglom, I. M. Problem 145 in Challenging Mathematical Problems with Elementary Solutions, Vol. 2. New York: Dover, 1987.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















