There are a number of formulas variously known as Hurwitz's formula.

The first is

where 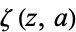 is a Hurwitz zeta function,  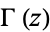is the gamma function, and  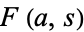is the periodic zeta function (Apostol 1995; 1997, p. 71).

Hurwitz has another formula, also known as Hurwitz's theorem or the Riemann-Hurwitz formula. Let 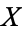 and 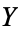 be compact Riemann surfaces, and suppose that there is a non-constant analytic map 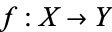. The Hurwitz formula gives the relationship between the genus of  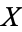and the genus of 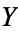, namely,

In this formula, 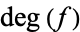 is the degree of the map. The degree of  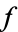is an integer  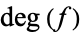such that for a generic point 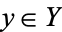, (i.e., for all but finitely many points in 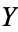), the set  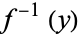consists of  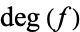points in 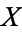. The sum  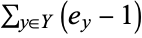in the Hurwitz formula can be viewed as a correction term to take into account the points where 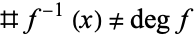. Such points are sometimes called branch points. The numbers  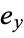are the ramification indices.

Hurwitz's theorem for Riemann surfaces essentially follows from an application of the polyhedral formula. It is used to find the genus of modular curves and hyperelliptic curves, and is often applied to find the genus of a complicated Riemann surface that happens to map to a simpler surface, usually the sphere.

REFERENCES:

Apostol, T. M. Theorem 12.6 in Introduction to Analytic Number Theory. New York: Springer-Verlag, 1995.

Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, 1997.

Jones, G. A. and Singerman, D. Complex Functions Cambridge, England: Cambridge University Press, p. 196, 1987.