Square Root Algorithms
المؤلف:
Flannery, S. and Flannery, D
المصدر:
In Code: A Mathematical Journey. London: Profile Books,
الجزء والصفحة:
...
4-9-2019
1528
Square Root Algorithms
A sequence of approximations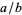 
to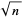 
can be derived by factoring
 |
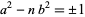(1)
|
(where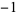 
is possible only if 
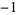is a quadratic residue of 
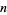). Then
 |
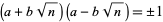(2)
|
 |
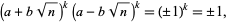(3)
|
and
Therefore,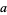 
and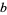 
are given by the recurrence relations
with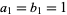 
. The error obtained using this method is
 |
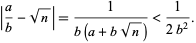(9)
|
The first few approximants to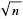 
are therefore given by
 |
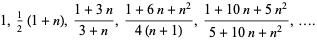(10)
|
This algorithm is sometimes known as the Bhaskara-Brouncker algorithm, and the approximants are precisely those obtained by taking successive convergents to the continued fraction of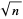 
. The fact that if 
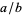is an approximation to 
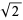, then 
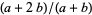is a better one (the 
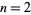case) was known to Theon of Smyrna in the second century AD (Wells 1986, p. 35).
Another general technique for deriving this sequence, known as Newton's iteration, is obtained by letting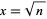 
. Then 
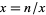, so the sequence
 |
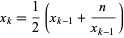(11)
|
converges quadratically to the root. The first few approximants to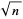 
are therefore given by
 |
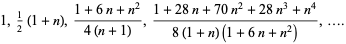(12)
|
Wolfram's iteration provides a method for finding square roots of integers using the binary representation.
REFERENCES:
Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, p. 132, 2000.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 34-35, 1986.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
