Zeilberger-Bressoud Theorem
المؤلف:
Andrews, G. E.
المصدر:
"Problems and Prospects for Basic Hypergeometric Functions." In The Theory and Application of Special Functions (Ed. R. Askey). New York: Academic Press
الجزء والصفحة:
...
2-9-2019
1479
Zeilberger-Bressoud Theorem
Dyson (1962abc) conjectured that the constant term in the Laurent series
 |
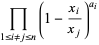(1)
|
is the multinomial coefficient
 |
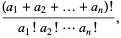(2)
|
based on a problem in particle physics. The theorem is called Dyson's conjecture, and was proved by Wilson (1962) and independently by Gunson (1962). A definitive proof was subsequently published by Good (1970).
A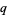 
-analog of this theorem (Andrews 1975) states that the coefficient of 
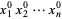in
 |
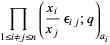(3)
|
where
![epsilon_(ij)=<span style=]() {1 for i<j; q for i>j " src="http://mathworld.wolfram.com/images/equations/Zeilberger-BressoudTheorem/NumberedEquation4.gif" style="height:41px; width:109px" /> |
(4)
|
is given by
 |
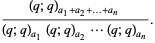(5)
|
This can also be stated in the form that the constant term of
 |
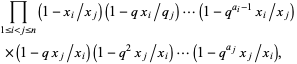(6)
|
is the q-multinomial coefficient
![([a_1+...+a_n]!)/([a_1]!...[a_n]!),](http://mathworld.wolfram.com/images/equations/Zeilberger-BressoudTheorem/NumberedEquation7.gif) |
(7)
|
where ![[n]!](http://mathworld.wolfram.com/images/equations/Zeilberger-BressoudTheorem/Inline3.gif)
is the q-factorial. The amazing proof of this theorem was given by Zeilberger and Bressoud (1985).
The full theorem reduces to Dyson's version when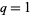 
. It also gives the q-analog of Dixon's theorem as
![sum_(k=-infty)^infty(-1)^kq^(k(3k+1)/2)[b+c; c+k]_q[c+a; a+k]_q[a+b; b+k]_q
=((q;q)_(a+b+c))/((q;q)_a(q;q)_b(q;q)_c)](http://mathworld.wolfram.com/images/equations/Zeilberger-BressoudTheorem/NumberedEquation8.gif) |
(8)
|
(Andrews 1975, 1986), where ![[n; k]_q](http://mathworld.wolfram.com/images/equations/Zeilberger-BressoudTheorem/Inline5.gif)
is a q-binomial coefficient. With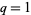 
and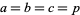 
, it gives the beautiful and well-known identity
 |
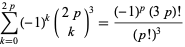(9)
|
(Andrews 1986).
REFERENCES:
Andrews, G. E. "Problems and Prospects for Basic Hypergeometric Functions." In The Theory and Application of Special Functions (Ed. R. Askey). New York: Academic Press, pp. 191-224, 1975.
Andrews, G. E. "The Zeilberger-Bressoud Theorem." §4.3 in q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 36-38, 1986.
Dyson, F. "Statistical Theory of the Energy Levels of Complex Systems. I." J. Math. Phys. 3, 140-156, 1962a.
Dyson, F. "Statistical Theory of the Energy Levels of Complex Systems. II." J. Math. Phys. 3, 157-165, 1962b.
Dyson, F. "Statistical Theory of the Energy Levels of Complex Systems. III." J. Math. Phys. 3, 166-175, 1962c.
Good, I. J. "Short Proof of a Conjecture by Dyson." J. Math. Phys. 11, 1884, 1970.
Gunson, J. "Proof of a Conjecture of Dyson in the Statistical Theory of Energy Levels." J. Math. Phys. 3, 752-753, 1962.
Wilson, K. G. "Proof of a Conjecture by Dyson." J. Math. Phys. 3, 1040-1043, 1962.
Zeilberger, D. and Bressoud, D. M. "A Proof of Andrews'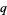 
-Dyson Conjecture." Disc. Math. 54, 201-224, 1985.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
