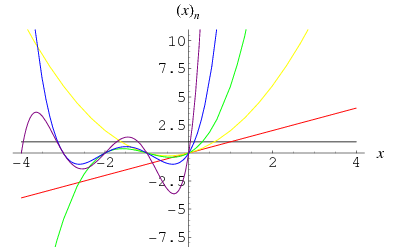
The Pochhammer symbol

			(1)
			(2)

(Abramowitz and Stegun 1972, p. 256; Spanier 1987; Koepf 1998, p. 5) for 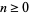 is an unfortunate notation used in the theory of special functions for the rising factorial, also known as the rising factorial power (Graham et al. 1994, p. 48) or ascending Factorial (Boros and Moll 2004, p. 16). The Pochhammer symbol is implemented in the Wolfram Language as Pochhammer[x, n].

In combinatorics, the notation 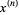 (Roman 1984, p. 5),  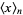(Comtet 1974, p. 6), or  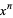(Graham et al. 1994, p. 48) is used for the rising factorial, while  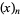or 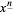 denotes the falling factorial (Graham et al. 1994, p. 48). Extreme caution is therefore needed in interpreting the notations  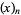and .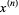

The first few values of 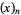 for nonnegative integers  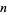are

			(3)
			(4)
			(5)
			(6)
			(7)

(OEIS A054654).

In closed form, 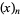 can be written

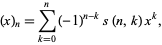(8)

where 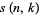 is a Stirling number of the first kind.

The Pochhammer symbol satisfies

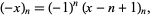(9)

the dimidiation formulas

			(10)
			(11)

and the duplications formula

{2^n(x)_(n/2)(x+1/2)_(n/2) for n even; 2^n(x)_((n+1)/2)(x+1/2)_((n-1)/2) for n odd " src="http://mathworld.wolfram.com/images/equations/PochhammerSymbol/NumberedEquation3.gif" style="height:58px; width:267px" />

(12)

(Boros and Moll 2004, p. 17).

A ratio of Pochhammer symbols is given in closed form by

{(x+m)_(n-m) if n>=m; 1/((x+n)_(m-n)) if n<=m " src="http://mathworld.wolfram.com/images/equations/PochhammerSymbol/NumberedEquation4.gif" style="height:64px; width:178px" />

(13)

(Boros and Moll 2004, p. 17).

The derivative is given by

(14)

where 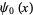 is the digamma function.

Special values include

			(15)
			(16)

The Pochhammer symbol 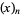 obeys the transformation due to Euler

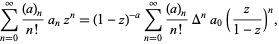(17)

where 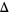 is the forward difference and

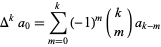(18)

(Nørlund 1955).

The sum of 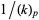 can be done in closed form as

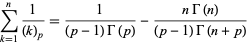(19)

for .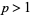

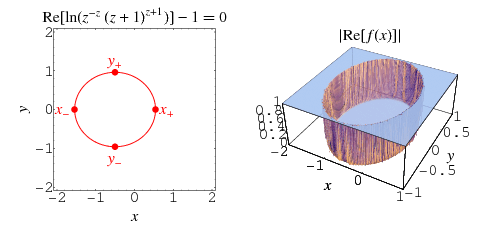
Consider the product

			(20)
			(21)

This function converges to 0, to a finite value, or diverges, depending on the value of 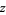. The critical curve is given by the implicit equation

(22)

Inside this curve, the function converges to 0, whereas outside it, it diverges. The maximum real value at which convergence occurs is given by 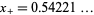 (OEIS A090462), and the minimum value by 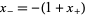. The extremal values of 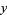are given by  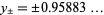(OEIS A090463). On the critical contour,  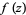takes on the value

(23)

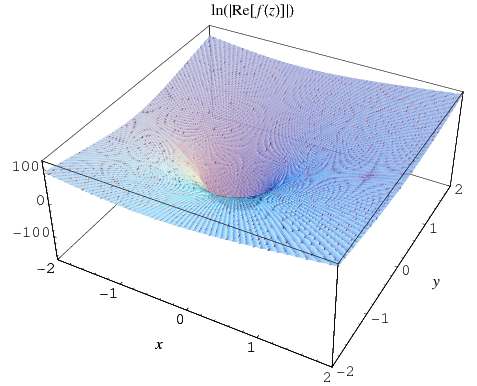
Plotting a suitably scaled version of 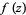 with 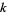 finite shows beautiful and subtle structures such as those illustrated above for  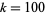(M. Trott, pers. comm., Dec. 1, 2003).

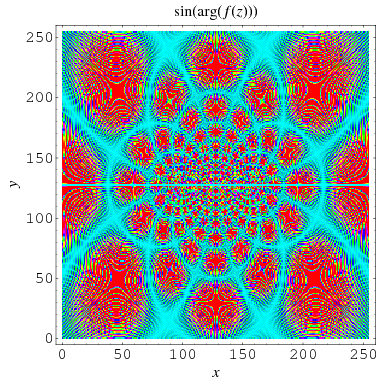
Another beautiful visualization plots 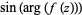, as illustrated above for  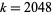(M. Trott, pers. comm., Dec. 2, 2003).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.

Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.

Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, 1974.

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 52, 1981.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.

Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, 1998.

Nørlund, N. E. "Hypergeometric Functions." Acta Math. 94, 289-349, 1955.

Roman, S. The Umbral Calculus. New York: Academic Press, p. 5, 1984.

Sloane, N. J. A. Sequences A054654, A090462, and A090463 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "The Pochhammer Polynomials 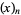." Ch. 18 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 149-165, 1987.