The parabolic cylinder functions are a class of functions sometimes called Weber functions. There are a number of slightly different definitions in use by various authors.

Whittaker and Watson (1990, p. 347) define the parabolic cylinder functions 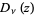 as solutions to the Weber differential equation

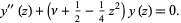(1)

The two independent solutions are given by 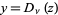 and 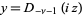, where

			(2)
			(3)

which, in the right half-plane , is equivalent to

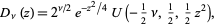(4)

where 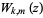 is the Whittaker function (Whittaker and Watson 1990, p. 347; Gradshteyn and Ryzhik 2000, p. 1018) and  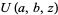is a confluent hypergeometric function of the first kind.

This function is implemented in the Wolfram Language as ParabolicCylinderD[nu, z].

For  a nonnegative integer 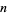, the solution  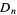reduces to

			(5)
			(6)

where 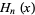 is a Hermite polynomial and  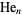is a modified Hermite polynomial. Special cases include

			(7)
			(8)

for , where 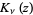 is an modified Bessel function of the second kind.

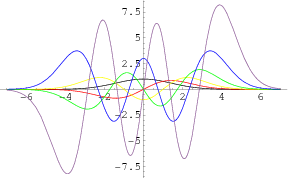
Plots of the function 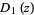 in the complex plane are shown above.

The parabolic cylinder functions 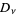 satisfy the recurrence relations

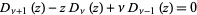(9)

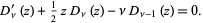(10)

The parabolic cylinder function for integral 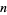 can be defined in terms of an integral by

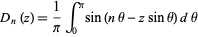(11)

(Watson 1966, p. 308), which is similar to the Anger function. The result

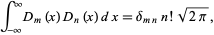(12)

where 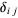 is the Kronecker delta, can also be used to determine the coefficients in the expansion

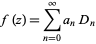(13)

as

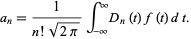(14)

For  real,

(15)

(Gradshteyn and Ryzhik 2000, p. 885, 7.711.3), where 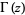 is the gamma function and  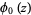is the polygamma function of order 0.

Abramowitz and Stegun (1972, p. 686) define the parabolic cylinder functions as solutions to

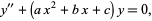(16)

sometimes called the parabolic cylinder differential equation (Zwillinger 1995, p. 414; Zwillinger 1997, p. 126). This can be rewritten by completing the square,

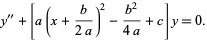(17)

Now letting

			(18)
			(19)

gives

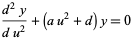(20)

where

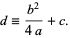(21)

Equation (◇) has the two standard forms

			(22)
			(23)

For a general 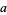, the even and odd solutions to (◇) are

			(24)
			(25)

where 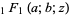 is a confluent hypergeometric function of the first kind. If  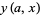is a solution to (22), then (23) has solutions

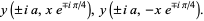(26)

Abramowitz and Stegun (1972, p. 687) define standard solutions to (◇) as

			(27)
			(28)

			(29)
			(30)
			(31)
			(32)

In terms of Whittaker and Watson's functions,

			(33)
			(34)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Parabolic Cylinder Function." Ch. 19 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 685-700, 1972.

Gradshteyn, I. S. and Ryzhik, I. M. "Parabolic Cylinder Functions" and "Parabolic Cylinder Functions 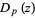" §7.7 and 9.24-9.25 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, pp. 835-842, 1018-1021, 2000.

Iyanaga, S. and Kawada, Y. (Eds.). "Parabolic Cylinder Functions (Weber Functions)." Appendix A, Table 20.III in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1479, 1980.

Jeffreys, H. and Jeffreys, B. S. "The Parabolic Cylinder, Hermite, and Hh Functions" et seq. §23.08-23.081 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 620-627, 1988.

Spanier, J. and Oldham, K. B. "The Parabolic Cylinder Function 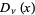." Ch. 46 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 445-457, 1987.

Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.

Whittaker, E. T. and Watson, G. N. "The Parabolic Cylinder Function." §16.5 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 347-348, 1990.

Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 414, 1995.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 126, 1997.