Clausen Formula
المؤلف:
Andrews, G. E. and Burge, W. H
المصدر:
"Determinant Identities." Pacific J. Math. 158,
الجزء والصفحة:
...
13-6-2019
1918
Clausen Formula
Clausen's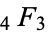 
identity
 |
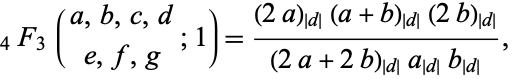(1)
|
holds for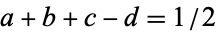 
, 
, 
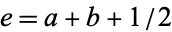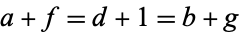, where 
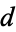a nonpositive integer and 
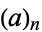is the Pochhammer symbol (Petkovšek et al. 1996). Closely related identities include
![_4F_3[1/2a,1/2(a+1),b+n,-n; 1/2b,1/2(b+1),a+1;1]=((b-a)_n)/((b)_n)](http://mathworld.wolfram.com/images/equations/ClausenFormula/NumberedEquation2.gif) |
(2)
|
and
![_4F_3[1/2a,1/2(a+1),b+n,-n; 1/2(b+1),1/2(b+2),a;1]=((b-a+1)_n)/((b+1)_(n-1)(b+2n))](http://mathworld.wolfram.com/images/equations/ClausenFormula/NumberedEquation3.gif) |
(3)
|
(Bailey 1935; Slater 1966, p. 245; Andrews and Burge 1993).
Another identity ascribed to Clausen which involves the hypergeometric function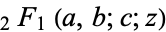 
and the generalized hypergeometric function 
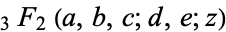is given by
![(_2F_1[a,b; a+b+1/2;x])^2=_3F_2[2a,a+b,2b; a+b+1/2,2a+2b;x]](http://mathworld.wolfram.com/images/equations/ClausenFormula/NumberedEquation4.gif) |
(4)
|
(Clausen 1828; Bailey 1935, p. 86; Hardy 1999, p. 106).
REFERENCES:
Andrews, G. E. and Burge, W. H. "Determinant Identities." Pacific J. Math. 158, 1-14, 1993.
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, 1935.
Clausen, T. "Ueber die Falle wenn die Reihe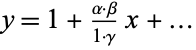 
ein quadrat von der Form 
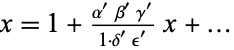hat." J. für Math. 3, 89-95, 1828.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, pp. 43 and 127, 1996.
Slater, L. J. Generalized Hypergeometric Functions. Cambridge, England: Cambridge University Press, 1966.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
