Incomplete Gamma Function
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
22-5-2019
2350
Incomplete Gamma Function
The "complete" gamma function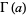 
can be generalized to the incomplete gamma function 
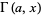such that 
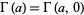. This "upper" incomplete gamma function is given by
 |
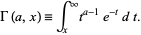(1)
|
For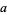 
an integer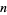 
where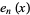 
is the exponential sum function. It is implemented as Gamma[a, z] in the Wolfram Language.
The special case of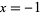 
can be expressed in terms of the subfactorial 
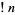as
 |
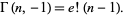(4)
|
The incomplete gamma function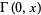 
has continued fraction
 |
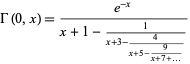(5)
|
(Wall 1948, p. 358).
The lower incomplete gamma function is given by
where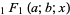 
is the confluent hypergeometric function of the first kind. For 
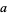an integer 
,
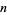It is implemented as Gamma[a, 0, z] in the Wolfram Language.
By definition, the lower and upper incomplete gamma functions satisfy
 |
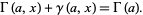(11)
|
The exponential integral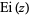 
is closely related to the incomplete gamma function 
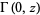by
![Gamma(0,z)=-Ei(-z)+1/2[ln(-z)-ln(-1/z)]-lnz.](http://mathworld.wolfram.com/images/equations/IncompleteGammaFunction/NumberedEquation5.gif) |
(12)
|
Therefore, for real 
,
![Gamma(0,x)=<span style=]() {-Ei(-x)-ipi for x<0; -Ei(-x) for x>0. " src="http://mathworld.wolfram.com/images/equations/IncompleteGammaFunction/NumberedEquation6.gif" style="height:41px; width:217px" /> |
(13)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 260, 1972.
Arfken, G. "The Incomplete Gamma Function and Related Functions." §10.5 in Mathematical Methods for Physicists, 3rd ed.Orlando, FL: Academic Press, pp. 565-572, 1985.
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
