Polynomial Map
المؤلف:
Becker, T. and Weispfenning, V.
المصدر:
Gröbner Bases: A Computational Approach to Commutative Algebra. New York: Springer-Verlag
الجزء والصفحة:
p. 330
13-2-2019
987
Polynomial Map
A map defined by one or more polynomials. Given a field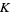 
, a polynomial map is a map 
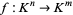such that for all points 
,
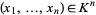for suitable polynomials ![g_1,...,g_m in K[X_1,...,X_n]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline4.gif)
. The zero set of 
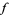is the set of all solutions of the simultaneous equations 
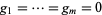, and is an algebraic variety in 
.
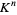An example of polynomial map is the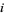 
th coordinate map 
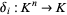, defined by 
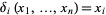for all 
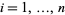. In the language of set theory, it is the projection of the Cartesian product 
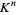onto the 
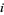th factor.
Polynomial maps can be defined on any nonempty subset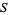 
of 
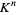. If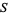 
is an affine variety, then the set of all polynomial maps from 
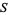to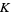 
is the coordinate ring ![K[S]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline19.gif)
of 
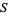. If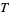 
is an affine variety of 
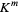, then every polynomial map 
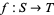induces a ring homomorphism ![F:K[T]->K[S]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline24.gif)
, defined by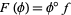 
. Conversely, every ring homomorphism ![G:K[T]->K[S]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline26.gif)
determines a polynomial map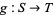 
, where 
.
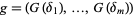A polynomial map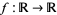 
is a real-valued polynomial function. Its graph is the plane algebraic curve with Cartesian equation 
.
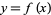REFERENCES:
Becker, T. and Weispfenning, V. Gröbner Bases: A Computational Approach to Commutative Algebra. New York: Springer-Verlag, p. 330, 1993.
الاكثر قراءة في مواضيع عامة في الجبر
اخر الاخبار
اخبار العتبة العباسية المقدسة
