Green,s Function--Poisson,s Equation
المؤلف:
Arfken, G
المصدر:
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
الجزء والصفحة:
pp. 485-486, 905, and 912
26-12-2018
945
Green's Function--Poisson's Equation
Poisson's equation is
 |
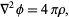(1)
|
where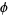 
is often called a potential function and 
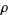a density function, so the differential operator in this case is 
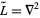. As usual, we are looking for a Green's function 
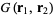such that
 |
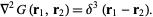(2)
|
But from Laplacian,
 |
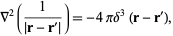(3)
|
so
 |
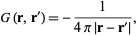(4)
|
and the solution is
 |
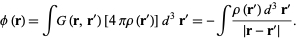(5)
|
Expanding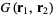 
in the spherical harmonics 
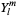gives
 |
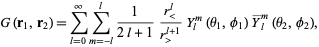(6)
|
where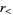 
and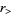 
are greater than/less than symbols. this expression simplifies to
 |
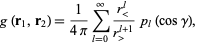(7)
|
where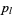 
are Legendre polynomials, and 
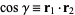. Equations (6) and (7) give the addition theorem for Legendre polynomials.
In cylindrical coordinates, the Green's function is much more complicated,
 |
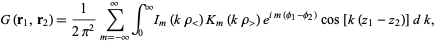(8)
|
where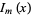 
and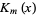 
are modified Bessel functions of the first and second kinds (Arfken 1985).
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 485-486, 905, and 912, 1985.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
