Integration by Parts
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.New York: Dover
الجزء والصفحة:
...
17-9-2018
2860
Integration by Parts
Integration by parts is a technique for performing indefinite integration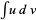 
or definite integration 
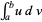by expanding the differential of a product of functions 
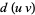and expressing the original integral in terms of a known integral 
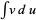. A single integration by parts starts with
 |
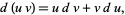(1)
|
and integrates both sides,
 |
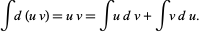(2)
|
Rearranging gives
 |
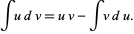(3)
|
For example, consider the integral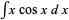 
and let
 |
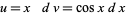(4)
|
 |
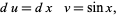(5)
|
so integration by parts gives
where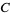 
is a constant of integration.
The procedure does not always succeed, since some choices of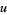 
may lead to more complicated integrals than the original. For example, consider again the integral 
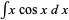and let
 |
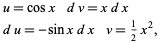(8)
|
giving
which is more difficult than the original (Apostol 1967, pp. 218-219).
Integration by parts may also fail because it leads back to the original integral. For example, consider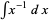 
and let
 |
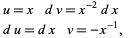(11)
|
then
 |
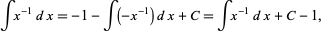(12)
|
which is same integral as the original (Apostol 1967, p. 219).
The analogous procedure works for definite integration by parts, so
 |
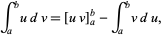(13)
|
where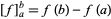 
.
Integration by parts can also be applied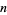 
times to 
:
 |
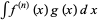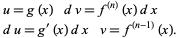(14)
|
Therefore,
 |
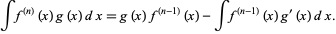(15)
|
But
 |
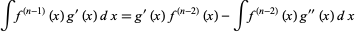(16)
|
 |
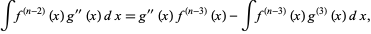(17)
|
so
 |
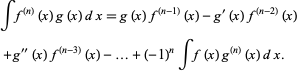(18)
|
Now consider this in the slightly different form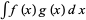 
. Integrate by parts a first time
 |
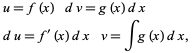(19)
|
so
 |
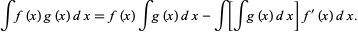(20)
|
Now integrate by parts a second time,
 |
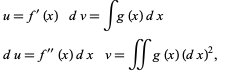(21)
|
so
 |
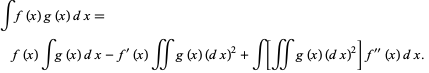(22)
|
Repeating a third time,
 |
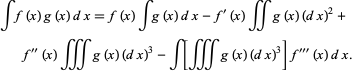(23)
|
Therefore, after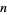 
applications,
 |
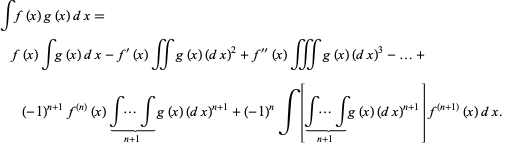(24)
|
If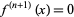 
(e.g., for an 
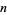th degree polynomial), the last term is 0, so the sum terminates after 
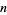terms and
 |
(25)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.New York: Dover, p. 12, 1972.
Apostol, T. M. "Integration by Parts." §5.9 in Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, pp. 217-220, 1967.
Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. New York: Springer-Verlag, p. 269, 1997.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
