
Unit Square Integral
 المؤلف:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H
المؤلف:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H
 المصدر:
Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
المصدر:
Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 17-9-2018
17-9-2018
 4641
4641
Unit Square Integral
Integrals over the unit square arising in geometric probability are
![int_0^1int_0^1sqrt(x^2+y^2)dxdy=1/3[sqrt(2)+sinh^(-1)(1)]
int_0^1int_0^1sqrt((x-1/2)^2+(y-1/2)^2)dxdy
=1/6[sqrt(2)+sinh^(-1)(1)],](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/NumberedEquation1.gif) |
(1)
|
which give the average distances in square point picking from a point picked at random in a unit square to a corner and to the center, respectively.
Unit square integrals involving the absolute value are given by
for ![R[n]>-1](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline7.gif) and
and ![R[n]>-2](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline8.gif) , respectively.
, respectively.
Another simple integral is given by
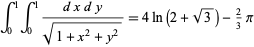 |
(4)
|
(Bailey et al. 2007, p. 67). Squaring the denominator gives
(OEIS A093754; M. Trott, pers. comm.), where 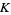 is Catalan's constant and
is Catalan's constant and 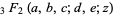 is a generalized hypergeometric function. A related integral is given by
is a generalized hypergeometric function. A related integral is given by
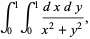 |
(10)
|
which diverges in the Riemannian sense, as can quickly seen by transforming to polar coordinates. However, taking instead Hadamard integral to discard the divergent portion inside the unit circle gives
(OEIS A093753), where 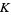 is Catalan's constant.
is Catalan's constant.
A collection of beautiful integrals over the unit square are given by Guillera and Sondow (2005) that follow from the general integrals
for 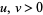 ,
, ![R[s]>-2](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline46.gif) if
if 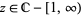 , and
, and ![R[s]>-1](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline48.gif) if
if 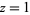 , where
, where 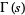 is the gamma function and
is the gamma function and 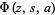 is the Lerch transcendent. In (15), to handle the case
is the Lerch transcendent. In (15), to handle the case 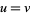 , take the limit as
, take the limit as 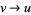 , which gives (16).
, which gives (16).
Another result is
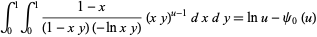 |
(17)
|
(Guillera and Sondow 2005), for 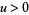 and where
and where 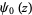 is the digamma function.
is the digamma function.
Guillera and Sondow (2005) also give
where the first holds for ![R[s]>-1](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline65.gif) , the second and third for
, the second and third for ![R[s]>-2](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline66.gif) ,
, 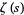 is the Riemann zeta function,
is the Riemann zeta function, 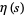 is the Dirichlet eta function, and
is the Dirichlet eta function, and 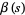 is the Dirichlet beta function. (19) was found by Hadjicostas (2002) for
is the Dirichlet beta function. (19) was found by Hadjicostas (2002) for 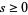 an integer. Formulas (18) and (19) are special cases of (16) obtained by setting
an integer. Formulas (18) and (19) are special cases of (16) obtained by setting 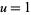 then taking
then taking 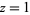 and
and 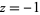 , respectively.
, respectively.
The beautiful formulas
were given by Beukers (1979). These integrals are special cases of (19) obtained by taking 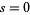 and 1, respectively. An analog involving Catalan's constant
and 1, respectively. An analog involving Catalan's constant 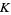 is given by
is given by
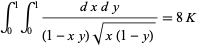 |
(23)
|
(Zudilin 2003).
Other beautiful integrals related to Hadjicostas's formula are given by
(Sondow 2003, 2005; Borwein et al. 2004, p. 49), where 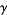 is the Euler-Mascheroni constant.
is the Euler-Mascheroni constant.
A collection of other special cases (Guillera and Sondow 2005) includes
where 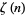 is the Riemann zeta function,
is the Riemann zeta function, 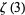 is Apéry's constant,
is Apéry's constant, 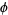 is the golden ratio,
is the golden ratio, 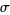 is Somos's quadratic recurrence constant, and
is Somos's quadratic recurrence constant, and 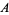 is the Glaisher-Kinkelin constant. Equation (57) appears in Sondow (2005), but is a special case of the type considered by Guillera and Sondow (2005).
is the Glaisher-Kinkelin constant. Equation (57) appears in Sondow (2005), but is a special case of the type considered by Guillera and Sondow (2005).
Corresponding single integrals over ![[0,1]](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline196.gif) for most of these integrals can be found by making the change of variables
for most of these integrals can be found by making the change of variables 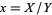 ,
, 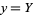 . The Jacobian then gives
. The Jacobian then gives 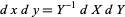 , and the new limits of integration are
, and the new limits of integration are ![<span style=]() {X,0,1}" src="http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline200.gif" style="height:14px; width:50px" />,
{X,0,1}" src="http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline200.gif" style="height:14px; width:50px" />, ![<span style=]() {Y,X,1}" src="http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline201.gif" style="height:14px; width:52px" />. Doing the integral with respect to
{Y,X,1}" src="http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline201.gif" style="height:14px; width:52px" />. Doing the integral with respect to 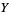 then gives a 1-dimensional integral over
then gives a 1-dimensional integral over ![[0,1]](http://mathworld.wolfram.com/images/equations/UnitSquareIntegral/Inline203.gif) . For details, see the first part of the proof of Guillera-Sondow's Theorem 3.1.
. For details, see the first part of the proof of Guillera-Sondow's Theorem 3.1.
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Beukers, F. "A Note on the Irrationality of 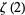 and
and 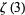 ." Bull. London Math. Soc. 11, 268-272, 1979.
." Bull. London Math. Soc. 11, 268-272, 1979.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005. http://arxiv.org/abs/math.NT/0506319.
Hadjicostas, P. "Some Generalizations of Beukers' Integrals." Kyungpook Math. J. 42, 399-416, 2002.
Sloane, N. J. A. Sequences A093753 and A093754 in "The On-Line Encyclopedia of Integer Sequences."
Sondow, J. "Criteria for Irrationality of Euler's Constant." Proc. Amer. Math. Soc. 131, 3335-3344, 2003. http://arxiv.org/abs/math.NT/0209070.
Sondow, J. "Double Integrals for Euler's Constant and 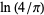 and an Analog of Hadjicostas's Formula." Amer. Math. Monthly 112, 61-65, 2005.
and an Analog of Hadjicostas's Formula." Amer. Math. Monthly 112, 61-65, 2005.
Zudilin, W. "An Apéry-Like Difference Equation for Catalan's Constant." Electronic J. Combinatorics 10, No. 1, R14, 1-10, 2003. http://www.combinatorics.org/Volume_10/Abstracts/v10i1r14.html.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


