Triangle Line Picking
المؤلف:
Sloane, N. J. A
المصدر:
Sequences A093063, A093064, A180307, and A180308 in "The On-Line Encyclopedia of Integer Sequences."
الجزء والصفحة:
...
17-9-2018
2528
Triangle Line Picking
Consider the average length of a line segment determined by two points picked at random in the interior of an arbitrary triangle. This problem is not affine, so a simple formula in terms of the area or linear properties of the original triangle apparently does not exist.
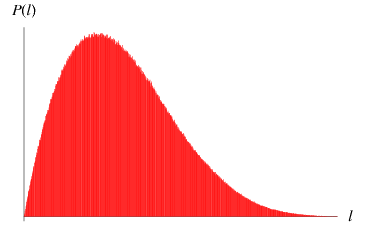
However, if the original triangle is chosen to be an isosceles right triangle with unit legs, then the average length of a line with endpoints chosen at random inside it is given by
(OEIS A093063; M. Trott, pers. comm., Mar. 10, 2004), which is numerically surprisingly close to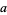 
.
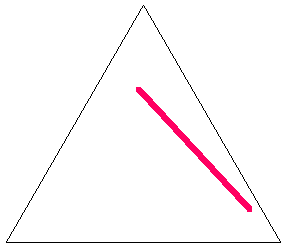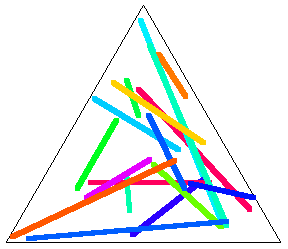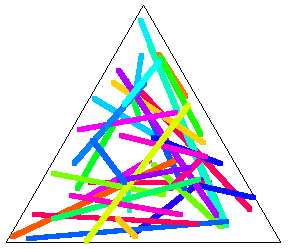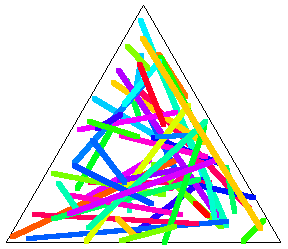
Similarly, if the original triangle is chosen to be an equilateral triangle with unit side lengths, then the average length of a line with endpoints chosen at random inside it is given by
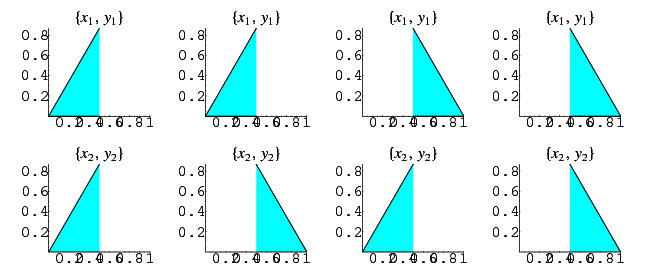
The integrand can be split up into the four pieces
As illustrated above, symmetry immediately gives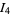 
and 
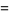, so
 |
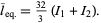(10)
|
With some effort, the integrals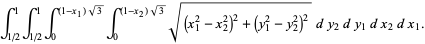 
and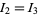 
can be done analytically to give the final beautiful result
(OEIS A093064; E. W. Weisstein, Mar. 16, 2004).
The mean length of a line segment picked at random in a 3, 4, 5 triangle is given by
(E. W. Weisstein, Aug. 6-9, 2010; OEIS A180307).
The mean length of a line segment picked at random in a 30-60-90 triangle was computed by E. W. Weisstein (Aug. 5, 2010) as a complicated analytic expression involving sums of logarithms. After simplification, the result can be written as
(E. Weisstein, M. Trott, A. Strzebonski, pers. comm., Aug. 25, 2010; OEIS A180308).
REFERENCES:
Sloane, N. J. A. Sequences A093063, A093064, A180307, and A180308 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
