
Log Gamma Function
 المؤلف:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H.
المؤلف:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H.
 المصدر:
Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
المصدر:
Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 21-8-2018
21-8-2018
 2291
2291
Log Gamma Function
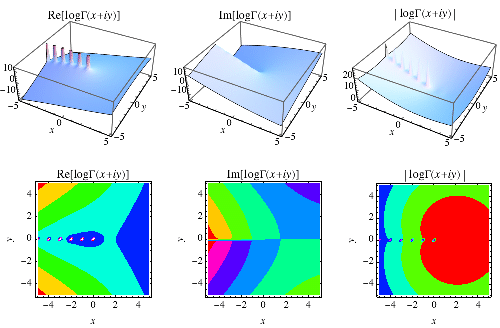
The plots above show the values of the function obtained by taking the natural logarithm of the gamma function, 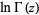 . Note that this introduces complicated branch cut structure inherited from the logarithm function.
. Note that this introduces complicated branch cut structure inherited from the logarithm function.
 |
|
|
For this reason, the logarithm of the gamma function is sometimes treated as a special function in its own right, and defined differently from 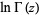 . This special "log gamma" function is implemented in the Wolfram Language as LogGamma[z], plotted above. As can be seen, the two definitions have identical real parts, but differ markedly in their imaginary components. Most importantly, although the log gamma function and
. This special "log gamma" function is implemented in the Wolfram Language as LogGamma[z], plotted above. As can be seen, the two definitions have identical real parts, but differ markedly in their imaginary components. Most importantly, although the log gamma function and 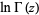 are equivalent as analytic multivalued functions, they have different branch cut structures and a different principal branch, and the log gamma function is analytic throughout the complex
are equivalent as analytic multivalued functions, they have different branch cut structures and a different principal branch, and the log gamma function is analytic throughout the complex 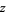 -plane except for a single branch cutdiscontinuity along the negative real axis. In particular, the log gamma function allows concise formulation of many identities related to the Riemann zeta function
-plane except for a single branch cutdiscontinuity along the negative real axis. In particular, the log gamma function allows concise formulation of many identities related to the Riemann zeta function 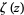 .
.
The log gamma function can be defined as
![lnGamma(z)=-gammaz-lnz+sum_(k=1)^infty[z/k-ln(1+z/k)].](http://mathworld.wolfram.com/images/equations/LogGammaFunction/NumberedEquation1.gif) |
(1)
|
(Boros and Moll 2004, p. 204). Another sum is given by
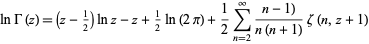 |
(2)
|
(Whittaker and Watson 1990, p. 261), where 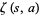 is a Hurwitz zeta function.
is a Hurwitz zeta function.
The second of Binet's log gamma formulas is
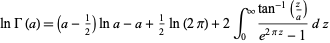 |
(3)
|
for ![R[a]>0](http://mathworld.wolfram.com/images/equations/LogGammaFunction/Inline7.gif) (Whittaker and Watson 1990, p. 251). Another formula for
(Whittaker and Watson 1990, p. 251). Another formula for 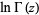 is given by Malmstén's formula.
is given by Malmstén's formula.
Integrals of 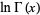 include
include
(OEIS A075700; Bailey et al. 2007, p. 179), which was known to Euler, and
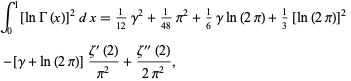 |
(7)
|
(OEIS A102887; Espinosa and Moll 2002, 2004; Boros and Moll 2004, p. 203; Bailey et al. 2007, p. 179), where 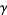 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 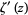 is the derivative of the Riemann zeta function.
is the derivative of the Riemann zeta function.
![int_0^1[lnGamma(x)]^3dx](http://mathworld.wolfram.com/images/equations/LogGammaFunction/Inline21.gif) is considered by Espinosa and Moll (2006) who, however, were not able to establish a closed form (Bailey et al. 2006, p. 181).
is considered by Espinosa and Moll (2006) who, however, were not able to establish a closed form (Bailey et al. 2006, p. 181).
Another integral is given by
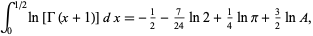 |
(8)
|
where 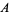 is the Glaisher-Kinkelin constant (Glaisher 1878).
is the Glaisher-Kinkelin constant (Glaisher 1878).
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Boros, G. and Moll, V. "The Expansion of the Loggamma Function." §10.6 in Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, pp. 201-203, 2004.
Espinosa, O. and Moll, V. "On Some Definite Integrals Involving the Hurwitz Zeta Function. Part I." Ramanujan J. 6, 159-188, 2002.
Espinosa, O. and Moll, V. "A Generalized Polygamma Function." Integral Transforms Spec. Funct. 15, 101-115, 2004.
Espinosa, O. and Moll, V. "The Evaluation of Tornheim Double Sums. I." J. Number Th. 116, 200-229, 2006.
Glaisher, J. W. L. "On the Product 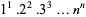 ." Messenger Math. 7, 43-47, 1878.
." Messenger Math. 7, 43-47, 1878.
Sloane, N. J. A. Sequences A075700 and A102887 in "The On-Line Encyclopedia of Integer Sequences."
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


