Infinite Cosine Product Integral
المؤلف:
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W.
المصدر:
"Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113
الجزء والصفحة:
...
21-8-2018
2714
Infinite Cosine Product Integral
At the age of 17, Bernard Mares proposed the definite integral (Borwein and Bailey 2003, p. 26; Bailey et al. 2006)
(OEIS A091473). Although this is within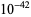 
of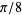 
,
 |
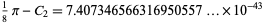(3)
|
(OEIS A091494), it is not equal to it. Apparently, no closed-form solution is known for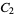 
.
Interestingly, the integral
(Borwein et al. 2004, pp. 101-102) has a value fairly close to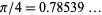 
, but no other similar relationships seem to hold for other multipliers of the form 
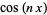or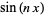 
.
The identity
 |
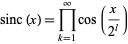(6)
|
can be expanded to yield
 |
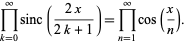(7)
|
In fact,
 |
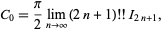(8)
|
where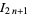 
is a Borwein integral.
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006b.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Sloane, N. J. A. Sequences A091473 and A091494 in "The On-Line Encyclopedia of Integer Sequences."
Trott, M. "The Mathematica Guidebooks Additional Material: Infinite Cosine Product Integral." http://www.mathematicaguidebooks.org/additions.shtml#N_2_01.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
