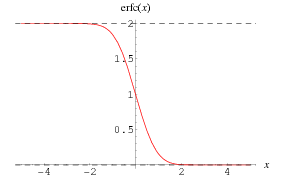
Erfc is the complementary error function, commonly denoted 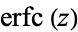, is an entire function defined by

			(1)
			(2)

It is implemented in the Wolfram Language as Erfc[z].

Note that some authors (e.g., Whittaker and Watson 1990, p. 341) define 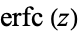 without the leading factor of .

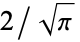For ,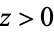

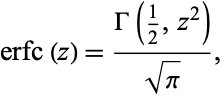(3)

where 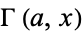 is the incomplete gamma function.

The derivative is given by

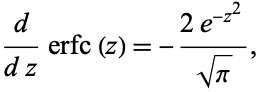(4)

and the indefinite integral by

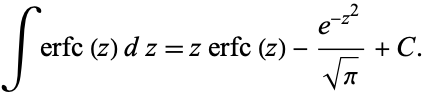(5)

It has the special values

			(6)
			(7)
			(8)

It satisfies the identity

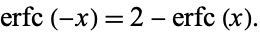(9)

It has definite integrals

			(10)
			(11)
			(12)

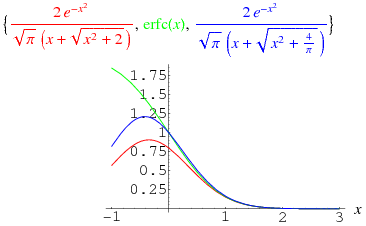
For 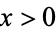,  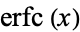is bounded by

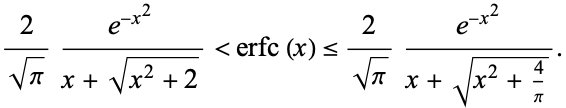(13)

Min   Max       Re       Im

Erfc can also be extended to the complex plane, as illustrated above.

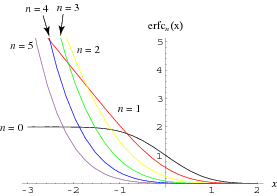
A generalization is obtained from the erfc differential equation

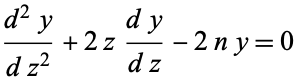(14)

(Abramowitz and Stegun 1972, p. 299; Zwillinger 1997, p. 122). The general solution is then

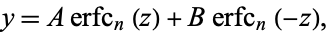(15)

where 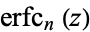 is the repeated erfc integral. For integer ,

			(16)
			(17)
			(18)
			(19)

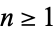(Abramowitz and Stegun 1972, p. 299), where 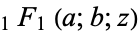 is a confluent hypergeometric function of the first kind and  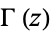is a gamma function. The first few values, extended by the definition for  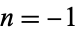and 0, are given by

			(20)
			(21)
			(22)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Repeated Integrals of the Error Function." §7.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 299-300, 1972.

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 568-569, 1985.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function." §6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 209-214, 1992.

Spanier, J. and Oldham, K. B. "The Error Function 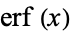 and Its Complement 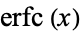" and "The  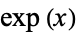and 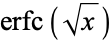 and Related Functions." Chs. 40 and 41 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393 and 395-403, 1987.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 122, 1997