Cantor Function
المؤلف:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H
المصدر:
Experimental Mathematics in Action.Wellesley, MA: A K Peters
الجزء والصفحة:
...
18-8-2018
3183
Cantor Function
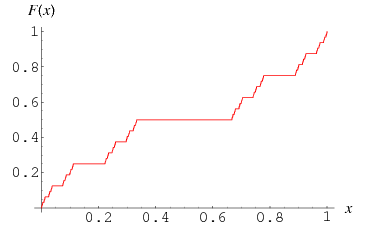
The Cantor function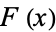 
is defined as the function on ![[0,1]](http://mathworld.wolfram.com/images/equations/CantorFunction/Inline2.gif)
such that for values of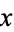 
on the Cantor set, i.e.,
 |
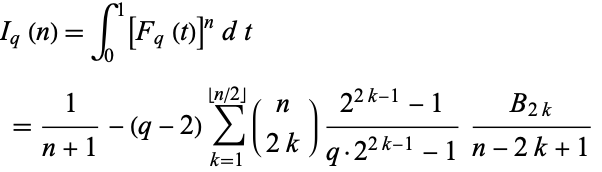(1)
|
then
 |
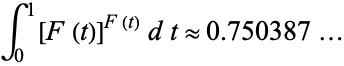(2)
|
which is then extended to other values by noting that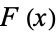 
is monotone and has the same values on each removed endpoint (Chalice 1991).
The Cantor function is a particular case of a devil's staircase (Devaney 1987, p. 110), and can be extended to a function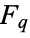 
for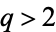 
, with 
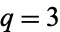corresponding to the usual Cantor function (Gorin and Kukushkin 2004).
Chalice (1991) showed that any real-valued functio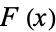n 
on ![[0,1]](http://mathworld.wolfram.com/images/equations/CantorFunction/Inline9.gif)
which is monotone increasing and satisfies
1. 
,
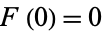2. 
,
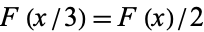3. 
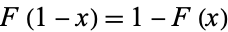
is the Cantor function (Chalice 1991; Wagon 2000, p. 132).
Gorin and Kukushkin (2004) give the remarkable identity
![I_q(n)=int_0^1[F_q(t)]^ndt
=1/(n+1)-(q-2)sum_(k=1)^(|_n/2_|)(n; 2k)(2^(2k-1)-1)/(q·2^(2k-1)-1)(B_(2k))/(n-2k+1)](http://mathworld.wolfram.com/images/equations/CantorFunction/NumberedEquation3.gif) |
(3)
|
for integer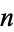 
. For 
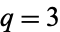and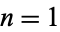 
, 2, ..., this gives the first few values as 1/2, 3/10, 1/5, 33/230, 5/46, 75/874, ... (OEIS A095844 and A095845).
M. Trott (pers. comm., June 8, 2004) has noted that
![int_0^1[F(t)]^(F(t))dt approx 0.750387...](http://mathworld.wolfram.com/images/equations/CantorFunction/NumberedEquation4.gif) |
(4)
|
(OEIS A113223), which seems to be just slightly greater than 3/4.
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action.Wellesley, MA: A K Peters, p. 237, 2007.
Chalice, D. R. "A Characterization of the Cantor Function." Amer. Math. Monthly 98, 255-258, 1991.
Devaney, R. L. An Introduction to Chaotic Dynamical Systems. Redwood City, CA: Addison-Wesley, 1987.
Gorin, E. A. and Kukushkin, B. N. "Integrals Related to the Cantor Function." St. Petersburg Math. J. 15, 449-468, 2004.
Sloane, N. J. A. Sequences A095844, A095845, A113223 in "The On-Line Encyclopedia of Integer Sequences."
Wagon, S. "The Cantor Function" and "Complex Cantor Sets." §5.2 and 5.3 in Mathematica in Action, 2nd ed. New York: W. H. Freeman, pp. 132-138, 2000.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
