
Beta Function
 المؤلف:
Abramowitz, M. and Stegun, I. A
المؤلف:
Abramowitz, M. and Stegun, I. A
 المصدر:
"Beta Function" and "Incomplete Beta Function." §6.2 and 6.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
المصدر:
"Beta Function" and "Incomplete Beta Function." §6.2 and 6.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 16-8-2018
16-8-2018
 4086
4086
Beta Function
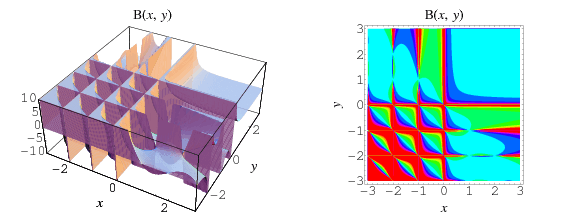
The beta function 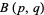 is the name used by Legendre and Whittaker and Watson (1990) for the beta integral (also called the Eulerian integral of the first kind). It is defined by
is the name used by Legendre and Whittaker and Watson (1990) for the beta integral (also called the Eulerian integral of the first kind). It is defined by
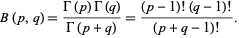 |
(1)
|
The beta function 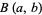 is implemented in the Wolfram Language as Beta[a, b].
is implemented in the Wolfram Language as Beta[a, b].
To derive the integral representation of the beta function, write the product of two factorials as
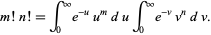 |
(2)
|
Now, let 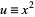 ,
, 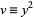 , so
, so
Transforming to polar coordinates with 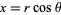 ,
, 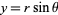
The beta function is then defined by
Rewriting the arguments then gives the usual form for the beta function,
By symmetry,
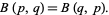 |
(13)
|
The general trigonometric form is
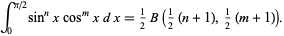 |
(14)
|
Equation (14) can be transformed to an integral over polynomials by letting 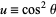 ,
,
For any 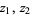 with
with ![R[z_1],R[z_2]>0](http://mathworld.wolfram.com/images/equations/BetaFunction/Inline51.gif) ,
,
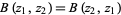 |
(19)
|
(Krantz 1999, p. 158).
To put it in a form which can be used to derive the Legendre duplication formula, let 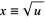 , so
, so 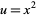 and
and 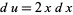 , and
, and
To put it in a form which can be used to develop integral representations of the Bessel functions and hypergeometric function, let 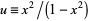 , so
, so
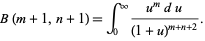 |
(22)
|
Derivatives of the beta function are given by
where 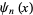 is the polygamma function.
is the polygamma function.
Various identities can be derived using the Gauss multiplication formula
Additional identities include
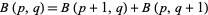 |
(32)
|
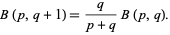 |
(33)
|
If 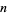 is a positive integer, then
is a positive integer, then
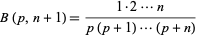 |
(34)
|
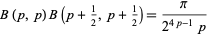 |
(35)
|
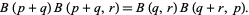 |
(36)
|
The beta function is also given by the product
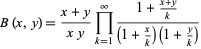 |
(37)
|
(Andrews et al. 1999, p. 8).
Gosper gave the general formulas
![product_(i=0)^(2n)B(i/(2n+1)+a,i/(2n+1)+b)
=((2n+1)^((2n+1)/2)pi^nB(n,1/2[(b+a)(2n+1)+1])B(a(2n+1),b(2n+1)))/((n-1)!)](http://mathworld.wolfram.com/images/equations/BetaFunction/NumberedEquation13.gif) |
(38)
|
for odd 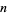 , and
, and
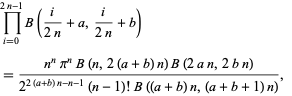 |
(39)
|
which are an immediate consequence of the analogous identities for gamma functions. Plugging 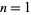 and
and 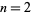 into the above give the special cases
into the above give the special cases
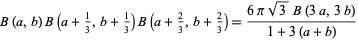 |
(40)
|
![B(a,b)B(a+1/4,b+1/4)B(a+1/2,b+1/2)B(a+3/4,b+3/4)
=(2^(3-4(a+b))pi^2B(4a,4b))/((a+b)[1+4(a+b)]B(2(a+b),2(a+b+1))).](http://mathworld.wolfram.com/images/equations/BetaFunction/NumberedEquation16.gif) |
(41)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Beta Function" and "Incomplete Beta Function." §6.2 and 6.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 258 and 263, 1972.
Andrews, G. E.; Askey, R.; and Roy, R. Special Functions. Cambridge, England: Cambridge University Press, 1999.
Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.
Arfken, G. "The Beta Function." §10.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 560-565, 1985.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The Beta Function." §1.5 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 9-13, 1981.
Jeffreys, H. and Jeffreys, B. S. "The Beta Function." §15.02 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 463-464, 1988.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 6-9, 1998.
Krantz, S. G. "The Beta Function." §13.1.11 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 157-158, 1999.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 425, 1953.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Gamma Function, Beta Function, Factorials, Binomial Coefficients" and "Incomplete Beta Function, Student's Distribution, F-Distribution, Cumulative Binomial Distribution." §6.1 and 6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 206-209 and 219-223, 1992.
Spanier, J. and Oldham, K. B. "The Incomplete Beta Function 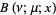 ." Ch. 58 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 573-580, 1987.
." Ch. 58 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 573-580, 1987.
Whittaker, E. T. and Watson, G. N. A Course of Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


