
Spherical Bessel Differential Equation
 المؤلف:
Abramowitz, M. and Stegun, I. A
المؤلف:
Abramowitz, M. and Stegun, I. A
 المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 5-7-2018
5-7-2018
 1725
1725
Spherical Bessel Differential Equation
Take the Helmholtz differential equation
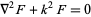 |
(1)
|
in spherical coordinates. This is just Laplace's equation in spherical coordinates with an additional term,
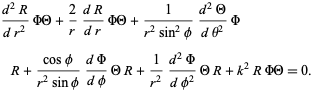 |
(2)
|
Multiply through by 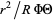 ,
,
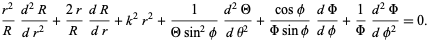 |
(3)
|
This equation is separable in 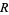 . Call the separation constant
. Call the separation constant 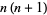 ,
,
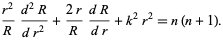 |
(4)
|
Now multiply through by 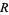 ,
,
![r^2(d^2R)/(dr^2)+2r(dR)/(dr)+[k^2r^2-n(n+1)]R=0.](http://mathworld.wolfram.com/images/equations/SphericalBesselDifferentialEquation/NumberedEquation5.gif) |
(5)
|
This is the spherical Bessel differential equation. It can be transformed by letting 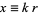 , then
, then
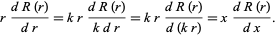 |
(6)
|
Similarly,
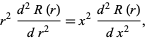 |
(7)
|
so the equation becomes
![x^2(d^2R)/(dx^2)+2x(dR)/(dx)+[x^2-n(n+1)]R=0.](http://mathworld.wolfram.com/images/equations/SphericalBesselDifferentialEquation/NumberedEquation8.gif) |
(8)
|
Now look for a solution of the form 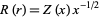 , denoting a derivative with respect to
, denoting a derivative with respect to  by a prime,
by a prime,
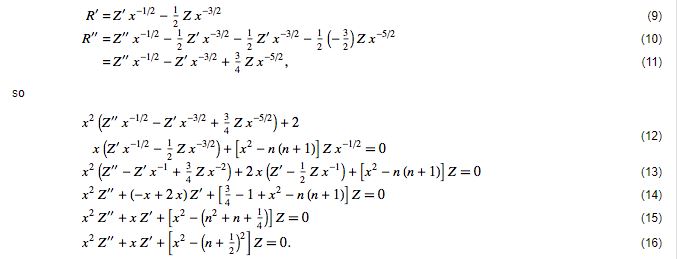
But the solutions to this equation are Bessel functions of half integral order, so the normalized solutions to the original equation are
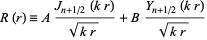 |
(17)
|
which are known as spherical Bessel functions. The two types of solutions are denoted 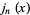 (spherical Bessel function of the first kind) or
(spherical Bessel function of the first kind) or 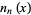 (spherical Bessel function of the second kind), and the general solution is written
(spherical Bessel function of the second kind), and the general solution is written
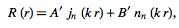
where
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 437, 1972.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 121, 1997.
 الاكثر قراءة في معادلات تفاضلية
الاكثر قراءة في معادلات تفاضلية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


