Partial derivatives are defined as derivatives of a function of multiple variables when all but the variable of interest are held fixed during the differentiation.

(1)

The above partial derivative is sometimes denoted 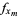 for brevity.

Partial derivatives can also be taken with respect to multiple variables, as denoted for examples

			(2)
			(3)
			(4)

Such partial derivatives involving more than one variable are called mixed partial derivatives.

For a "nice" two-dimensional function 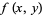 (i.e., one for which 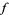, , 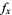, , 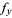 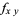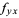exist and are continuous in a neighborhood ), then

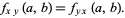(5)

More generally, for "nice" functions, mixed partial derivatives must be equal regardless of the order in which the differentiation is performed, so it also is true that

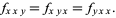(6)

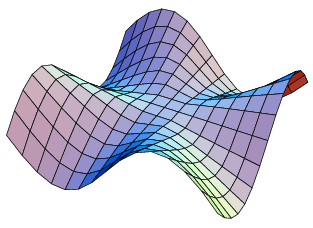
If the continuity requirement for mixed partials is dropped, it is possible to construct functions for which mixed partials are not equal. An example is the function

(7)

which has 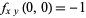 and 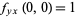 (Wagon 1991). This function is depicted above and by Fischer (1986).

Abramowitz and Stegun (1972) give finite difference versions for partial derivatives.

A differential equation expressing one or more quantities in terms of partial derivatives is called a partial differential equation. Partial differential equations are extremely important in physics and engineering, and are in general difficult to solve.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 883-885, 1972.

Fischer, G. (Ed.). Plate 121 in Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Bildband. Braunschweig, Germany: Vieweg, p. 118, 1986.

Thomas, G. B. and Finney, R. L. §16.8 in Calculus and Analytic Geometry, 9th ed. Reading, MA: Addison-Wesley, 1996.

Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 83-85, 1991.