The operator representing the computation of a derivative,

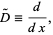(1)

sometimes also called the Newton-Leibniz operator. The second derivative is then denoted 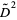, the third 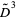, etc. The integral is denoted .

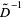The differential operator satisfies the identity

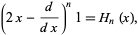(2)

where 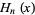 is a Hermite polynomial (Arfken 1985, p. 718), where the first few cases are given explicitly by

			(3)
			(4)
			(5)
			(6)
			(7)
			(8)

The symbol 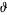 can be used to denote the operator

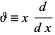(9)

(Bailey 1935, p. 8). A fundamental identity for this operator is given by

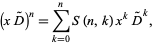(10)

where 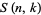 is a Stirling number of the second kind (Roman 1984, p. 144), giving

			(11)
			(12)
			(13)
			(14)

and so on (OEIS A008277). Special cases include

			(15)
			(16)
			(17)

A shifted version of the identity is given by

(18)

(Roman 1984, p. 146).

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.

Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: University Press, 1935.

Roman, S. The Umbral Calculus. New York: Academic Press, pp. 59-63, 1984.

Sloane, N. J. A. Sequence A008277 in "The On-Line Encyclopedia of Integer Sequences."