


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-3-2021
Date: 20-2-2021
Date: 16-2-2021
|
In statistics, sampling is the selection and implementation of statistical observations in order to estimate properties of an underlying population. Sampling is a vital part of modern polling, market research, and manufacturing, and its proper use is vital in the functioning of modern economies. The portion of a population selected for analysis is known as a sample, and the number of members in the sample is called the sample size.
The term "sampling" is also used in signal processing to refer to measurement of a signal at discrete times, usually with the intension of reconstructing the original signal. For infinite-precision sampling of a band-limited signal at the Nyquist frequency, the signal-to-noise ratio after 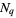 samples is
samples is
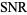 |
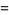 |
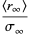 |
(1) |
 |
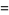 |
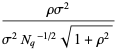 |
(2) |
 |
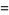 |
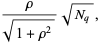 |
(3) |
where 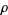 is the normalized correlation coefficient
is the normalized correlation coefficient
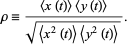 |
(4) |
For 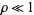 ,
,
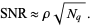 |
(5) |
The identical result is obtained for oversampling. For undersampling, the signal-to-noise ratio decreases (Thompson et al. 1986).
REFERENCES:
Feuer, A. Sampling in Digital Signal Processing and Control. Boston, MA: Birkhäuser, 1996.
Govindarajulu, Z. Elements of Sampling Theory and Methods. Upper Saddle River, NJ: Prentice-Hall, 1999.
Thompson, A. R.; Moran, J. M.; and Swenson, G. W. Jr. Interferometry and Synthesis in Radio Astronomy. New York: Wiley, pp. 214-216, 1986.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|