


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-1-2020
Date: 6-10-2020
Date: 12-9-2020
|
The integer sequence 1, 0, 1, 1, 2, 1, 3, 2, 4, 3, 5, 4, 7, 5, 8, 7, 10, 8, 12, 10, 14, 12, 16, 14, 19, 16, 21, 19, ... (OEIS A005044) given by the coefficients of the Maclaurin series for
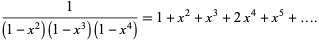 |
(1) |

A binary plot of the first few terms in the sequence is illustrated above.
Closed forms include
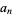 |
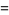 |
![1/(288){107+54n+6n^2+(-1)^n[81+18n+64cos(1/3pin)]+36[cos(1/2pin)-sin(1/2pin)]}](https://mathworld.wolfram.com/images/equations/AlcuinsSequence/Inline3.gif) |
(2) |
 |
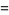 |
![1/(288){107+54n+6n^2+(-1)^n[81+18n+64cos(1/3pin)]](https://mathworld.wolfram.com/images/equations/AlcuinsSequence/Inline6.gif) |
(3) |
 |
 |
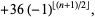 |
(4) |
where 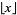 is the floor function.
is the floor function.
The number of different triangles which have integral sides and perimeter 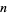 is given by
is given by
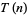 |
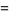 |
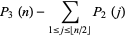 |
(5) |
 |
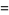 |
![[(n^2)/(12)]-|_n/4_||_(n+2)/4_|](https://mathworld.wolfram.com/images/equations/AlcuinsSequence/Inline17.gif) |
(6) |
 |
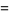 |
![{[(n^2)/(48)] for n even; [((n+3)^2)/(48)] for n odd,](https://mathworld.wolfram.com/images/equations/AlcuinsSequence/Inline20.gif) |
(7) |
where 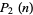 and
and 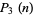 are partition functions, with
are partition functions, with 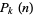 giving the number of ways of writing
giving the number of ways of writing 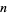 as a sum of
as a sum of 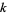 terms,
terms, ![[x]](https://mathworld.wolfram.com/images/equations/AlcuinsSequence/Inline26.gif) is the nearest integer function, and
is the nearest integer function, and 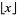 is the floor function (Jordan et al. 1979, Andrews 1979, Honsberger 1985). Strangely enough,
is the floor function (Jordan et al. 1979, Andrews 1979, Honsberger 1985). Strangely enough, 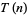 for
for 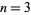 , 4, ... is precisely Alcuin's sequence.
, 4, ... is precisely Alcuin's sequence.
REFERENCES:
Andrews, G. "A Note on Partitions and Triangles with Integer Sides." Amer. Math. Monthly 86, 477, 1979.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 39-47, 1985.
Jordan, J. H.; Walch, R.; and Wisner, R. J. "Triangles with Integer Sides." Amer. Math. Monthly 86, 686-689, 1979.
Sloane, N. J. A. Sequence A005044/M0146 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|