


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-2-2021
Date: 21-1-2021
Date: 23-9-2020
|
A number of the form
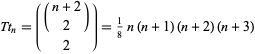 |
(Comtet 1974, Stanley 1999), where 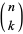 is a binomial coefficient. The first few values are 3, 15, 45, 105, 210, 378, 630, ... (OEIS A050534). The generating function for the tritriangular numbers is
is a binomial coefficient. The first few values are 3, 15, 45, 105, 210, 378, 630, ... (OEIS A050534). The generating function for the tritriangular numbers is
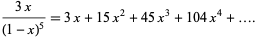 |
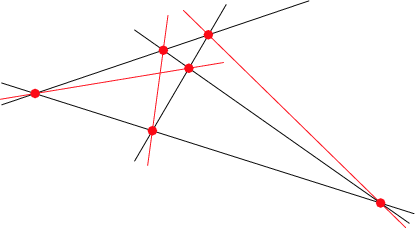
Given 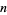 lines in a plane, no two of which are parallel, and no three of which are concurrent, draw lines pairwise through their points of intersection. The number of new lines drawn is then
lines in a plane, no two of which are parallel, and no three of which are concurrent, draw lines pairwise through their points of intersection. The number of new lines drawn is then 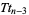 (Schmall 1915).
(Schmall 1915).
REFERENCES:
Comtet, L. Problem 1. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 72, 1974.
Schmall, C. N. "Problem 432." Amer. Math. Monthly 22, 130, 1915.
Sloane, N. J. A. Sequence A050534 in "The On-Line Encyclopedia of Integer Sequences."
Stanley, R. P. Problem 5.5, Case 2 in Enumerative Combinatorics, Vol. 2. Cambridge, England: Cambridge University Press, 1999.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|