المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Beta Integral |
 1527
 04:42 مساءً
date: 21-5-2019 |
Author : Whittaker, E. T. and Watson, G. N 
Book or Source : A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990. 
Page and Part : ...|
Read More
Date: 18-8-2018
1250
Date: 19-9-2018
3609
Date: 27-4-2018
2183
|
The integral
 |
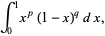called the Eulerian integral of the first kind by Legendre and Whittaker and Watson (1990). The solution is the beta function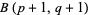 
.
REFERENCES:
Gasper, G. "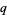
-Extensions of Barnes', Cauchy's, and Euler's Beta Integrals." In Topics in Mathematical Analysis (Ed. Yh. M. Rassias). London: World Scientific, pp. 194-314, 1989.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
