x

هدف البحث
بحث في العناوين
بحث في المحتوى
بحث في اسماء الكتب
بحث في اسماء المؤلفين

اختر القسم
موافق


تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
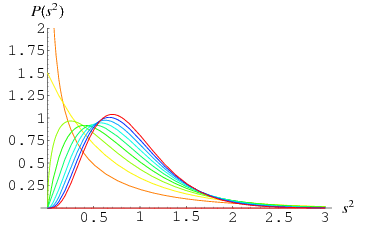
Sample Variance Distribution
المؤلف:
Kenney, J. F. and Keeping, E. S
المصدر:
Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
الجزء والصفحة:
...
24-2-2021
1064
Let 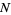 samples be taken from a population with central moments
samples be taken from a population with central moments 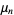 . The sample variance
. The sample variance 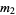 is then given by
is then given by
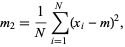 |
(1) |
where 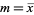 is the sample mean.
is the sample mean.
The expected value of 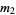 for a sample size
for a sample size 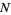 is then given by
is then given by
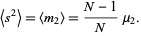 |
(2) |
Similarly, the expected variance of the sample variance is given by
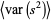 |
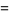 |
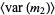 |
(3) |
 |
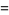 |
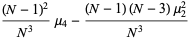 |
(4) |
(Kenney and Keeping 1951, p. 164; Rose and Smith 2002, p. 264).
The algebra of deriving equation (4) by hand is rather tedious, but can be performed as follows. Begin by noting that
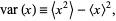 |
(5) |
so
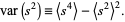 |
(6) |
The value of 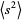 is already known from equation (◇), so it remains only to find
is already known from equation (◇), so it remains only to find 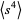 . The algebra is simplified considerably by immediately transforming variables to
. The algebra is simplified considerably by immediately transforming variables to 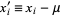 and performing computations with respect to these central variables. Since the variance does not depend on the mean
and performing computations with respect to these central variables. Since the variance does not depend on the mean 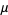 of the underlying distribution, the result obtained using the transformed variables will give an identical result while immediately eliminating expectation values of sums of terms containing odd powers of
of the underlying distribution, the result obtained using the transformed variables will give an identical result while immediately eliminating expectation values of sums of terms containing odd powers of 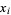 (which equal 0). To determine
(which equal 0). To determine 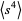 , expand equation (6) to obtain
, expand equation (6) to obtain
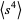 |
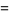 |
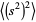 |
(7) |
 |
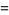 |
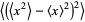 |
(8) |
 |
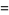 |
![<[1/Nsumx_i^2-(1/Nsumx_i)^2]^2>](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline27.gif) |
(9) |
 |
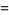 |
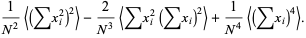 |
(10) |
Working on the first term of (10),
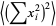 |
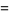 |
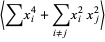 |
(11) |
 |
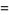 |
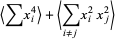 |
(12) |
 |
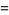 |
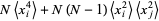 |
(13) |
 |
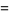 |
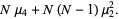 |
(14) |
The second term of (◇) is given by
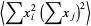 |
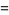 |
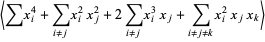 |
(15) |
 |
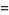 |
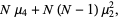 |
(16) |
and the third term by
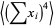 |
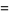 |
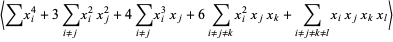 |
(17) |
 |
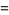 |
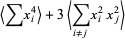 |
(18) |
 |
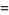 |
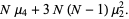 |
(19) |
Plugging (◇)-(19) into (◇) then gives
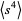 |
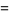 |
![1/(N^2)[Nmu_4+N(N-1)mu_2^2]-2/(N^3)[Nmu_4+N(N-1)mu_2^2]+1/(N^4)[Nmu_4+3N(N-1)mu_2^2]](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline60.gif) |
(20) |
 |
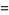 |
![(1/N-2/(N^2)+1/(N^3))mu_4+[(N-1)/N-(2(N-1))/(N^2)+(3(N-1))/(N^3)]mu_2^2](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline63.gif) |
(21) |
 |
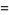 |
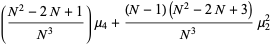 |
(22) |
 |
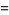 |
![((N-1)[(N-1)mu_4+(N^2-2N+3)mu_2^2])/(N^3)](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline69.gif) |
(23) |
(Kenney and Keeping 1951, p. 164). Plugging (◇) and (23) into (◇) then gives
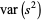 |
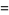 |
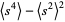 |
(24) |
 |
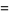 |
![((N-1)[(N-1)mu_4-(N-3)mu_2^2])/(N^3),](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline75.gif) |
(25) |
as before.
For a normal distribution, 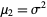 and
and 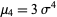 , so
, so
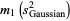 |
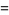 |
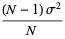 |
(26) |
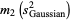 |
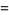 |
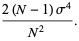 |
(27) |
The third ane fourth moments of 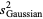 are given by
are given by
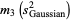 |
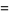 |
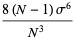 |
(28) |
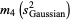 |
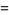 |
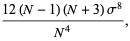 |
(29) |
giving the skewness and kurtosis excess of the distribution of the 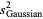 as
as
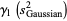 |
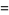 |
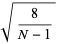 |
(30) |
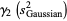 |
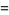 |
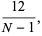 |
(31) |
as computed by Student. Student also conjectured that the underlying distribution is Pearson type III distribution
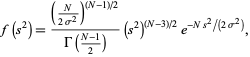 |
(32) |
where 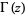 is the gamma function--a conjecture that was subsequently proven by R. A. Fisher. Curves are illustrated above for
is the gamma function--a conjecture that was subsequently proven by R. A. Fisher. Curves are illustrated above for 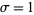 and
and 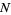 varying from
varying from 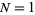 to 10.
to 10.
REFERENCES:
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Rose, C. and Smith, M. D. Mathematical Statistics with Mathematica. New York: Springer-Verlag, 2002.