


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 29-2-2016
التاريخ: 14-3-2016
التاريخ: 9-3-2016
التاريخ: 15-10-2015
|
معكوس المصفوفة
سنناقش في هذا البند بعض خواص عمليات المصفوفات الجبرية، وسوف نلاحظ أن عددا من القواعد الأساسية الحسابية للأعداد الحقيقية تنطبق على المصفوفات عدا بعض منها.
خواص عمليات المصفوفات:
إذا كانت a و b أعداد حقيقية فإن ab = ba (قانون التبديل في الضرب) إلا أن هذه الخاصية قد لا تتحقق في ضرب المصفوفات . أي إذا A وB مصفوفتان فإن AB ≠ BA حتى إذا كانت AB و BA معرفتان ولهما نفس السعة.
مثال(1):
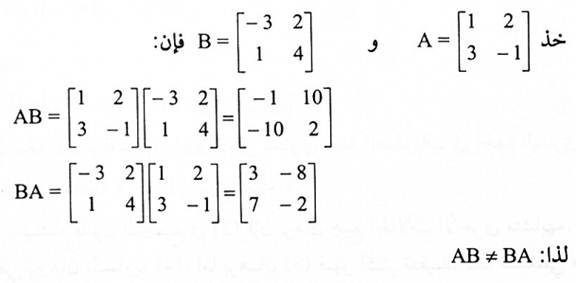
مبرهنة (1-1):
إذا كانت سعة كل من المصفوفات A و B و C تلائم العمليات إزائها فإن خواص المصفوفات الآتية تكون متحققة:
A + B = B +A .1 (قانون التبديل).
2. A + (B+C) = (A+B) + C (قانون التجميع).
3. A (BC) = (AB) C (قانون التجميع بالضرب).
4.A (B+C) = AB + AC (التوزيع من اليسار).
5. (A+B)C = AC + BC (التوزيع من اليمين).
6. A (B-C) = AB = AC.
7. (B-C)A = BA - CA
8. a(B+C) = aB - aC
9. a(B-C) = aB - aC
10. (a + b)C = aC = bC
11. (a – b)C = aC - bC
12. a(bC) = (ab) C
13. a(BC) = (aB)C = B (aC)
البرهان :
لبرهان المتساويات أعلاه يجب أن نبين:
1- أن سعة المصفوفات في الجهة اليمنى تساوي سعة المصفوفات في الجهة اليسرى.
2- العناصر المتقابلة في كلا الجانبين متساوية.
باستثناء قانون التجميع في (3) فإن برهان جميع الحالات الأخرى متشابهة. لذا سنكتفي ببرهان المتساوية (4)، أما برهان (3) فهو اكثر تعقيداً لذا سنعطي مثالاً يوضحها.
نثبت اولاً ان A (B+C) = AB + AC لتكوين A (B + C) يجب أن تكون المصفوفتان B و C لهما نفس السعة لنقل m x n، عليه فإن عدد أعمدة A يجب أن يكون m، فسعة A يجب أن تكون بالشكل r x m هذا سيجعل A(B+C). إذا A (B + C) و AB + AC لهما نفس السعة.
لتكن 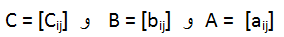 ، نريد ان نبرهن أن العناصر المتقابلة في A(B+C) و AB + AC متساوية. أي أن:
، نريد ان نبرهن أن العناصر المتقابلة في A(B+C) و AB + AC متساوية. أي أن:
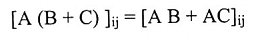
لكل قيم i و j .
من عمليات جمع وضرب المصفوفات نحصل على:
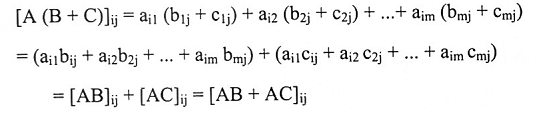
ملاحظة:
العنصر في A الذي يقع في الصف رقم i والعمود رقم j يكتب بالشكل [Aij ]
مثال (2):
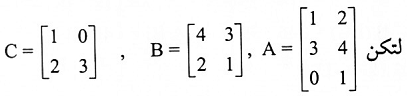
فإن:
A(B+C) = AB + AC
الحل:
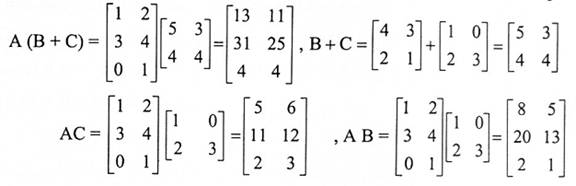
عليه A(B+C) = AB + AC
مثال (3):
باعتبار المصفوفات في المثال (2) حقق صحة:
A(BC) = (AB)C
الحل:
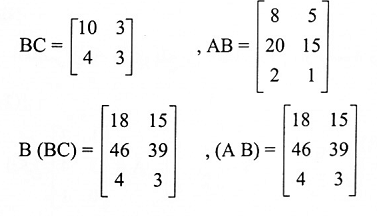
إذن
A(BC) = (AB) = c
المصفوفة الصفرية : هي المصفوفة التي جميع عناصرها أصفاراً.
مثال (4):

هي أمثلة على المصفوفة الصفرية.
ملاحظة:
لا يتحقق قانون الاختصار في المصفوفات بصورة عامة، أي إذا كانت C,B,A مصفوفات فليس صحيحاً اختصار A من العلاقة AB = AC لكي نحصل على B = C كذلك AB = 0 مع ذلك A ≠ 0 , B ≠ 0
مثال (5):
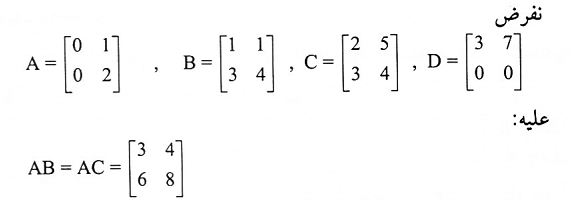
مع أن A ≠ 0
فإن اختصار A لا يعطي B = C وكذلك AD = 0 مع أن A ≠ 0 و D ≠ 0
مبرهنة (1-2):
بفرض سعة المصفوفات تحقق العمليات المؤشرة إزاءها فإن المتساويات الآتية متحققة.
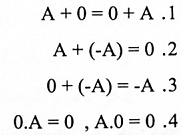
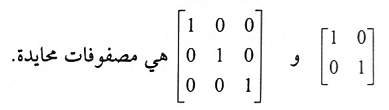
المصفوفة المحايدة: تسمى المصفوفة محايدة إذا كانت مربعة وجميع عناصرها في القطر الرئيسي تساوي 1 وبقية العناصر أصفار، يرمز للمصفوفة المحايدة بالرمز In ، وسعتها n × n
مثال (6):
تعريف (1-3):
لتكن A مصفوفة مربعة و B مصفوفة لها نفس سعة A. يقال للمصفوفة A بأنها قابلة للانعكاس إذا تحقق الشرط الآتي:
AB = BA = In
وتسمى B معكوس A
يرمز لمعكوس A بالرمز A-1 وتصبح العلاقة أعلاه:
AA-1=A-1A=In
مثال (7):

هو معكوس A لأن:
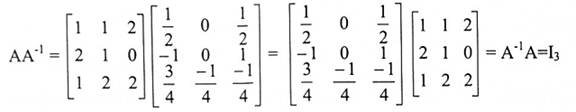
عليه فإن A قابلة للانعكاس.
مبرهنة (1-4):
إذا كانت كل من B و C معكوس A فإن B = C.
البرهان:
بما أن B معكوس A فإن BA = In
وبالضرب في C نحصل على:
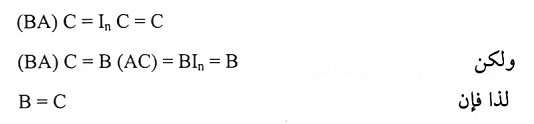
مبرهنة (1-5):
إذا كانت A و B مصفوفتان لهما نفس السعة وقابلتان للانعكاس فإن:
AB.1 قابلة للانعكاس.
2. (AB)-1 = B-1 A-1
البرهان:
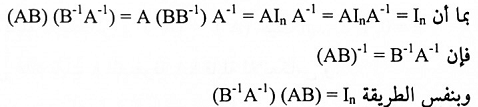
يمكن تعميم المبرهنة أعلاه لثلاث أو أكثر من العوامل، أي أن معكوس ضرب أي عدد منتهي من المصفوفات هو حاصل ضرب المعكوسات بترتيب معاكسة ، بمعنى آخر:
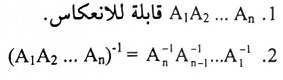
تعريف (1-6):
إذا كانت A مصفوفة مربعة فإن:

علاوة على ذلك ، إذا كانت A قابلة للانعكاس فإن:
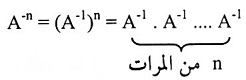
مبرهنة (1-7):
إذا كانت A مصفوفة مربعة و m و n أعداد صحيحة فإن:
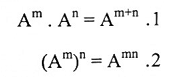
مرهنة (1-8):
لتكن A قابلة للانعكاس
1. A-1 قابلة للانعكاس و A = (A-1)-1
2. An قابلة للانعكاس و (An) = (A-1)n حيث n = 0,1,2,…, n
3. لكل عدد ثابت k المصفوفة KA قابلة للانعكاس و :
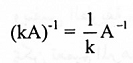
البرهان:
1. بما أن AA-1 = A-1A = In فإن A-1 قابلة لانعكاس ، و (A-1) = A(برهن).
2. لما كانت A-n = An-n = Ao = I لذا "A قابلة للانعكاس.

3. نفرض K ≠ 0. من المبرهنة (1-1):
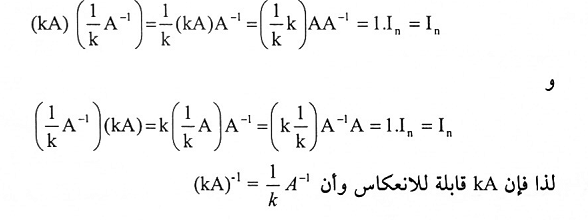
مثال (8):
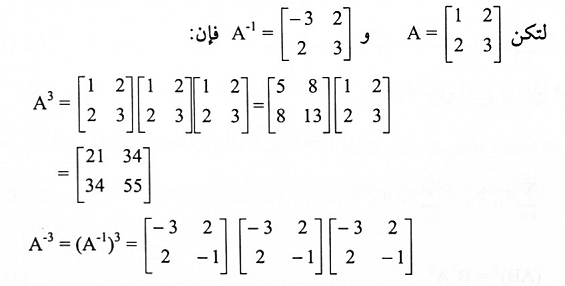
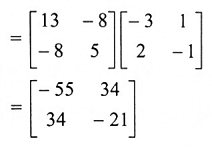
مبرهنة (1-9):
(خواص منقولة المصفوفة): إذا كانت سعة كل من AوB تلائم العمليات إزاءها فإن:

البرهان :
1. تطبق مباشر على تعريف المنقولة.
4. نفرض أن سعة المصفوفة هي m x n وسعة B هي n x p وبما أن سعة A B هي m x p (لماذا؟) فإن سعة (AB)T هي p x m والآن عنصر (AB)T في الموقع ij يساوي عنصر AB في الموقع ji ويساوي :

ملاحظة: يمكن تعميم الفقرة (4) من المبرهنة ((1-7 لأكثر من مصفوفتين، أي أن:
منقولة حاصل ضرب أي عدد منتهي من المصفوفات يساوي حاصل ضرب منقولاتها بترتيب معكوس جبرياً تكتب:
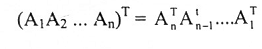
مبرهنة (1-8):
إذا كانت A مصفوفة قابلة للانعكاس فإن AT قابلة للانعكاس و

البرهان:
من المبرهنة (1-7):
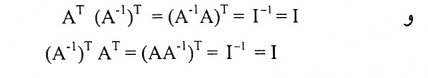
مثال (9):
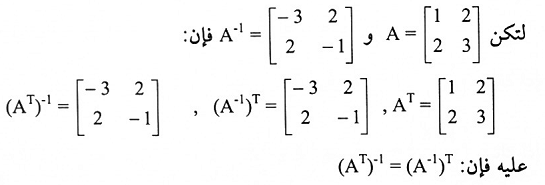
متعددة الحدود المتضمنة مصفوفات:
إذا كانت A مصفوفة سعتها m x n و P(x) أي متعددة حدود
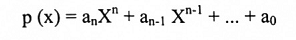
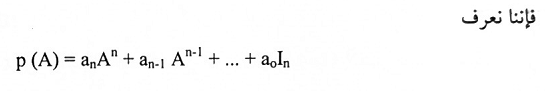
مثال (10):
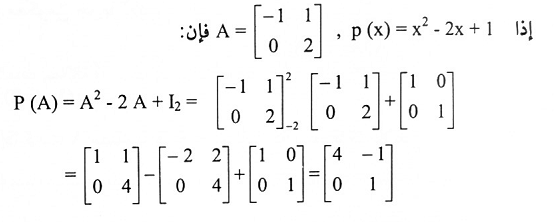



|
|
|
|
صنع الذكريات والتفكير يدمر الدماغ.. دراسة تشرح السبب
|
|
|
|
|
|
|
الصين.. عودة كاسحتي الجليد إلى شنغهاي بعد انتهاء بعثة استكشافية إلى القطب الجنوبي
|
|
|
|
|
|
جامعة الكفيل تكرم الفائزين بأبحاث طلبة كلية الصيدلة وطب الأسنان
|
|
|
|
مشروع التكليف الشرعي بنسخته السادسة الورود الفاطمية... أضخم حفل لفتيات كربلاء
|
|
|
|
ضمن جناح جمعيّة العميد العلميّة والفكريّة المجمع العلمي يعرض إصداراته في معرض تونس الدولي للكتاب
|
|
|
|
جامعة الكفيل تعقد مؤتمرها الطلابي العلمي الرابع
|